Advertisements
Advertisements
Question
Find the Median of the following distribution:
| x | 3 | 5 | 10 | 12 | 8 | 15 |
| f | 2 | 4 | 6 | 10 | 8 | 7 |
Solution
Arranging the terms in ascending order and preparing the cumulative frequency table:
| x | f | c.f. |
| 3 | 2 | 2 |
| 5 | 4 | 6 |
| 8 | 8 | 14 |
| 10 | 6 | 20 |
| 12 | 10 | 30 |
| 15 | 7 | 37 |
Here, n = 37 which is odd.
So Median = `(("n" + 1)/2)^"th" "term"`
= `((37 + 1)/2)^"th" "term"`
= `(38/2)^"th"`
= 19th term
Hence, Median is the value of the 9th term = 10.
APPEARS IN
RELATED QUESTIONS
Compute the median for the following data:
| Marks | No. of students |
| More than 150 | 0 |
| More than 140 | 12 |
| More than 130 | 27 |
| More than 120 | 60 |
| More than 110 | 105 |
| More than 100 | 124 |
| More than 90 | 141 |
| More than 80 | 150 |
A student got the following marks in 9 questions of a question paper.
3, 5, 7, 3, 8, 0, 1, 4 and 6.
Find the median of these marks.
Estimate the median for the given data by drawing an ogive:
| Class | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency | 4 | 9 | 15 | 14 | 8 |
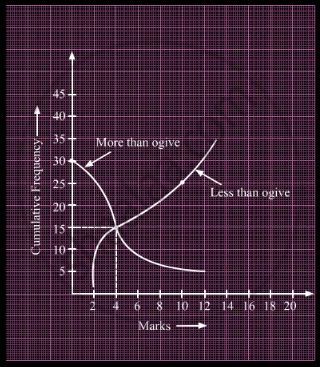
What is the value of the median of the data using the graph in the following figure of less than ogive and more than ogive?
A student draws a cumulative frequency curve for the marks obtained by 40 students of a class as shown below. Find the median marks obtained by the students of the class.

If 35 is removed from the data: 30, 34, 35, 36, 37, 38, 39, 40, then the median increased by
Calculate the median of the following distribution:
| No. of goals | 0 | 1 | 2 | 3 | 4 | 5 |
| No. of matches | 2 | 4 | 7 | 6 | 8 | 3 |
The median of the following observations 11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24. Find the value of x and hence find the mean.
The median of the following data is 525. Find the values of x and y, if the total frequency is 100.
| Class interval | Frequency |
| 0 – 100 | 2 |
| 100 – 200 | 5 |
| 200 – 300 | x |
| 300 – 400 | 12 |
| 400 – 500 | 17 |
| 500 – 600 | 20 |
| 600 – 700 | y |
| 700 – 800 | 9 |
| 800 – 900 | 7 |
| 900 – 1000 | 4 |
If in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately ______.
