Advertisements
Advertisements
Question
If 12cosecθ = 13, find the value of `(sin^2θ - cos^2θ) /(2sinθ cosθ) xx (1)/tan^2θ`.
Solution
12cosecθ = 13
⇒ cosecθ = `(13)/(12)`
⇒ sinθ = `(12)/(13) = "Perpendicular"/"Hypotenuse"`
⇒ Base
= `sqrt(("Hypotenuse")^2 - ("Perpendicular")^2`
= `sqrt((13)^2 - (12)^2`
= `sqrt(169 - 144)`
= `sqrt(25)`
= 5
cosθ = `"Base"/"Hypotenuse" = (5)/(13)`
tanθ= `"Perpendicular"/"Base" = (12)/(5)`
Now, `(sin^2θ - cos^2θ) /(2sinθ cosθ) xx (1)/tan^2θ`
= `((12/13)^2 - (5/13)^2)/(2(12/13)(5/13)) xx (1)/(12/5)^2`
= `(144/169 - 25/169)/(120/169) xx (25)/(144)`
= `(119)/(120) xx (25)/(144)`
= `(595)/(3456)`.
APPEARS IN
RELATED QUESTIONS
In the given figure, AD is perpendicular to BC. Find: 5 cos x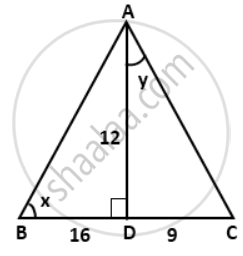
In the given figure, AD is perpendicular to BC. Find: 15 tan y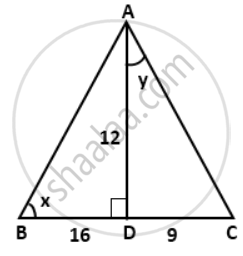
In the given figure, AD is perpendicular to BC. Find:
`(3)/("sin" x) + (4)/("cos" y) - 4 "tan" y`
In a right-angled triangle ABC, ∠B = 90°, BD = 3, DC = 4, and AC = 13. A point D is inside the triangle such as ∠BDC = 90°.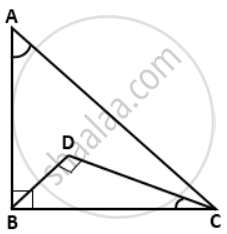
Find the values of 2 tan ∠BAC - sin ∠BCD
If 4 sinθ = 3 cosθ, find tan2θ + cot2θ
If 3cosθ - 4sinθ = 2cosθ + sinθ, find tanθ.
If 4sinθ = `sqrt(13)`, find the value of `(4sinθ - 3cosθ)/(2sinθ + 6cosθ)`
If 35 sec θ = 37, find the value of sin θ - sin θ tan θ.
If cosecθ = `1(9)/(20)`, show that `(1 - sinθ + cosθ)/(1 + sinθ + cosθ) = (3)/(7)`
If 3 tanθ = 4, prove that `sqrt(secθ - "cosec"θ)/(sqrt(secθ - "cosec"θ)) = (1)/sqrt(7)`.
