Answer 1

Given: 4 tan θ = 3 ⇒ tan θ = 3/4

Let us suppose a right angle triangle ABC right angled at B, with one of the acute angle θ. Let the sides be BC = 3kand AB = 4k, where k is a positive number

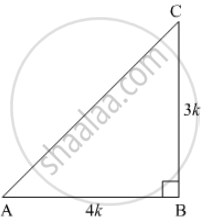
By Pythagoras theorem, we get

`AC^2 = BC^2 + AB^2`

`AC^2 = (3k)^2 + (4k)^2`

`AC^2 = 9k^2 + 16k^2`

`AC = sqrt(25k^2)`

`AC = +- 5k`

Ignoring AC = − 5k , as k is a positive number, we get

AC = 5k

if `tan theta  = (BC)/(AB) = 3/4` then `sin theta = (BC)/(AC) = 3/5` and `cos theta = (AB)/(AC) = 4/5` 

Putting the values in  `((4 sin theta - cos theta + 1)/(4 sin theta +  cos theta - 1))` we get

`((4xx3/5 - 4/5 + 1)/(4xx 3/5 + 4/5 -1)) = (((12- 4 + 5)/5)/((12 + 4 - 5)/5)) = 13/11`