Advertisements
Advertisements
Question
If 5tanθ = 12, find the value of `(2sinθ - 3cosθ)/(4sinθ - 9cosθ)`.
Solution
5tanθ = 12
⇒ tanθ = `(12)/(5) = "Perpendicular"/"Base"`
Hypotenuse
= `sqrt(("Perpendicular")^2 + ("Base")^2`
= `sqrt((12)^2 + (5)^2`
= `sqrt(144 + 25)`
= `sqrt(169)`
= 13
sinθ = `"Perpendicular"/"Hypotenuse" = (12)/(13)`, cosθ = `"Base"/"Hypotenuse" = (5)/(13)`
⇒ `(2sinθ - 3cosθ)/(4sinθ - 9cosθ)`
= `(2 xx 12/13 - 3 xx 5/13)/(4 xx 12/13 - 9 xx 5/13)`
= `(24 - 15)/(48 - 45)`
= `(9)/(3)`
= 3.
APPEARS IN
RELATED QUESTIONS
In tan θ = 1, find the value of 5cot2θ + sin2θ - 1.
In the given figure, ∠Q = 90°, PS is a median om QR from P, and RT divides PQ in the ratio 1 : 2. Find: `("tan" ∠"TSQ")/("tan"∠"PRQ")`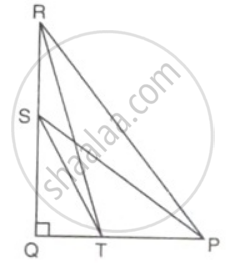
In the given figure, AD is perpendicular to BC. Find:
`(3)/("sin" x) + (4)/("cos" y) - 4 "tan" y`
In a right-angled triangle ABC, ∠B = 90°, BD = 3, DC = 4, and AC = 13. A point D is inside the triangle such as ∠BDC = 90°.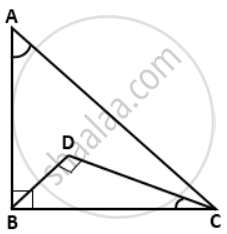
Find the values of 2 tan ∠BAC - sin ∠BCD
If 24cosθ = 7 sinθ, find sinθ + cosθ.
If 4sinθ = `sqrt(13)`, find the value of 4sin3θ - 3sinθ
If a cotθ = b, prove that `("a"sinθ - "b"cosθ)/("a"sinθ + "b"cosθ) = ("a"^2 - "b"^2)/("a"^2 + "b"^2)`
If cotθ = `sqrt(7)`, show that `("cosec"^2θ -sec^2θ)/("cosec"^2θ + sec^2θ) = (3)/(4)`
If 12 cotθ = 13, find the value of `(2sinθ cosθ)/(cos^2θ - sin^2θ)`.
If secA = `(17)/(8)`, verify that `(3 - 4sin^2 "A")/(4 cos^2 "A" - 3)= (3 - tan^2"A")/(1 - 3tan^2"A")`
