Advertisements
Advertisements
Question
If `veca = 3hati - 2hatj + hatk` and `vecb = 2hati - 4hatj - 3hatk` then the value of `|veca - 2vecb|` will be ______.
Options
`sqrt(85)`
`sqrt(86)`
`sqrt(87)`
`sqrt(88)`
Solution
If `veca = 3hati - 2hatj + hatk` and `vecb = 2hati - 4hatj - 3hatk` then the value of `|veca - 2vecb|` will be `underlinebb(sqrt(86))`.
Explanation:
Given, `veca = 3hati - 2hatj + hatk`
`vecb = 2hati - 4hatj - 3hatk`
Then, `(veca - 2vecb) = [(3hati - 2hatj + hatk) - 2(2hati - 4hatj - 3hatk)]`
= `[3hati - 2hati + hatk - 4hati + 8hati + 6hati]`
= `(-hati + 6hatj + 7hatk)`
`|veca - 2vecb| = sqrt((-1)^2 + (6)^2 + (7)^2)`
= `sqrt(1 + 36 + 49)`
= `sqrt(86)`
APPEARS IN
RELATED QUESTIONS
If `veca=4hati-hatj+hatk` then find a unit vector parallel to the vector `veca+vecb`
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = -hati + hatj - hatk`, find the unit vector in the direction of the vector `veca +vecb`.
Find a vector in the direction of vector `5hati - hatj +2hatk` which has a magnitude of 8 units.
Show that the direction cosines of a vector equally inclined to the axes OX, OY, and OZ are `pm1/sqrt3, 1/sqrt3, 1/sqrt3`.
Identify the unit vector in the following.
How do you deduce that two vectors are perpendicular?
The position vector particle has a length of 1m and makes 30° with the x-axis. What are the lengths of the x and y components of the position vector?
Compare the components for the following vector equations
(a) `"T"hatj - "mg"hatj = "ma"hatj`
(b) `vecT + vecF = vecA + vecB`
(c) `vecT - vecF = vecA - vecB`
(d) `"T"hatj + "mg"hatj = "ma"hatj`
If `overlinea`, `overlineb` and `overlinec` are three non-coplanar vectors then `(overlinea + overlineb + overlinec).[(overlinea + overlineb) xx (overlinea + overlinec)]` = ______
If `overline(a),overline(b),overline(c)` are non-coplanar vectors and λ is a real number then `[lambda(overline(a)+overline(b))lambda^2overline(b) lambda overline(c)]=[overline(a) overline(b)+overline(c) overline(b)]` for ______.
If the horizontal and vertical components of a force are negative, then that force is acting in between
Find the vector component of the vector with initial point (2, 1) and terminal point (–5, 7).
Unit vector perpendicular to the plane of the triangle ABC with position vectors `veca, vecb, vecc` of the vertices A, B, C is ______.
Two vectors `veca = a_1 hati + a_2 hatj + a_3 hatk` and `vecb = b_1 hati + b_2 hatj + b_3 hatk` are collinear if ______.
If `veca = 4hati + 6hatj` and `vecb = 3hatj + 4hatk`, then the vector form of the component of `veca` along `vecb` is ______.
Check whether the vectors `2hati +2hatj +3hatk,-3hati +3hatj +2hatk and 3hati + 4hatk` From a triangle or not.
If `4hati - 5hatj + hatk, 2hati + 3hatj + 3hatk` and `xhati + yhatj + zhatk` represent the sides AB, BC and AC respectively of a triangle ABC, then find x, y, z.
Check whether the vectors `2hati + 2hatj +3hatk, -3hati +3hatj +2hatk` and `3hati +4hatk` form a triangle or not.
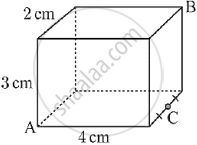
Shown below is a cuboid. Find `vec(BA).vec(BC)`
Check whether the vectors `2hati + 2hatj + 3hatk , -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
