Advertisements
Advertisements
Question
If cos(α + β) = `4/5` and sin(α – β) = `5/13`, where α lie between 0 and `pi/4`, find the value of tan2α.
[Hint: Express tan2α as tan(α + β + α – β)]
Solution
Given that: cos(α + β) = `4/5`
∴ tan(α + β) = `3/4`
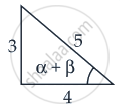
And sin(α – β) = `5/13`
∴ tan(α – β) = `5/12`
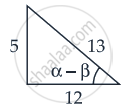
Now tan 2α = tan[α + β + α – β]
= tan[(α + β) + (α – β)]
= `(tan(alpha + beta) + tan(alpha - beta))/(1 - tan(alpha + beta).tan(alpha - beta))`
= `(3/4 + 5/12)/(1 - 3/4 xx 5/12)`
= `((9 + 5)/12)/((48 - 15)/48)`
= `14/12 xx 48/33`
= `56/33`
Hence, tan 2α = `56/33`.
APPEARS IN
RELATED QUESTIONS
Prove that `(tanA + secA - 1)/(tanA - secA + 1) = (1 + sinA)/cosA`
If `(2sinalpha)/(1 + cosalpha + sinalpha)` = y, then prove that `(1 - cosalpha + sinalpha)/(1 + sinalpha)` is also equal to y.
`["Hint": "Express" (1 - cosalpha + sinalpha)/(1 + sinalpha) = (1 - cosalpha + sinalpha)/(1 + sinalpha) * (1 + cosalpha + sinalpha)/(1 + cosalpha + sinalpha)]`
If m sinθ = n sin(θ + 2α), then prove that tan(θ + α)cotα = `(m + n)/(m - n)`
[Hint: Express `(sin(theta + 2alpha))/sintheta = m/n` and apply componendo and dividendo]
If tanx = `b/a`, then find the value of `sqrt((a + b)/(a - b)) + sqrt((a - b)/(a + b))`
Prove that cosθ `cos theta/2 - cos 3theta cos (9theta)/2` = sin 7θ sin 8θ.
[Hint: Express L.H.S. = `1/2[2costheta cos theta/2 - 2 cos 3theta cos (9theta)/2]`
If cosα + cosβ = 0 = sinα + sinβ, then prove that cos2α + cos2β = -2cos(α + β).
[Hint: (cosα + cosβ)2 - (sinα + sinβ)2 = 0]
Find the value of the expression `3[sin^4 ((3pi)/2 - alpha) + sin^4 (3pi + alpha)] - 2[sin^6 (pi/2 + alpha) + sin^6 (5pi - alpha)]`
cos2θ cos2Φ + sin2(θ – Φ) – sin2(θ + Φ) is equal to ______.
Given, `f_n(x) = 1/n(sin^nx + cos^nx)` for n = 1, 2, 3, ....... Then the value of 24(f4(x) – f6(x)) is equal to ______.
The value of cos 255° + sin 195° is ______.
The number of solution of tan x + sec x = 2 cos x in [0, 2π] is ______.
