Advertisements
Advertisements
Question
If the letters of the word ASSASSINATION are arranged at random. Find the probability that no two A’s are coming together
Solution
Total number of word is ASSASSINATION are 13.
Where, we have 3A’s, 4S’, 2I’s, 2N’s, 1T’s and 1O’s.
If no two A’s are together, then arranging the alphabets except A’s
– S – S – S – S – I – N – T – I – O – N –
Number of ways of arranging all alphabets except A’s
= `(10!)/(4!2!2!)`
There are 11 vacant places between these alphabets.
∴ 3 A’s can be placed in 11 places in 11C3 ways
= `(11!)/(3!8!)`
∴ Total number of words when no two A’s together
= `(11!)/(3!8!) xx (101)/(4!2!2!)`
∴ Required probability = `(11! xx 10!)/(3!8!4!2!2!) xx (4!3!2!2!)/(13!)`
= `(10!)/(8! xx 13 xx 12)`
= `(10 xx 9 xx 8!)/(8! xx 13 xx 12)`
= `(10 xx 9)/(13 xx 12)`
= `15/26`
APPEARS IN
RELATED QUESTIONS
Which of the following can not be valid assignment of probabilities for outcomes of sample space S = {ω1, ω2,ω3,ω4,ω5,ω6,ω7}
| Assignment | ω1 | ω2 | ω3 | ω4 | ω5 | ω6 | ω7 |
| (a) | 0.1 | 0.01 | 0.05 | 0.03 | 0.01 | 0.2 | 0.6 |
| (b) | `1/7` | `1/7` | `1/7` | `1/7` | `1/7` | `1/7` | `1/7` |
| (c) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
| (d) | –0.1 | 0.2 | 0.3 | 0.4 | -0.2 | 0.1 | 0.3 |
| (e) | `1/14` | `2/14` | `3/14` | `4/14` | `5/14` | `6/14` | `15/14` |
A card is selected from a pack of 52 cards.
- How many points are there in the sample space?
- Calculate the probability that the card is an ace of spades.
- Calculate the probability that the card is
- an ace
- black card.
A fair coin is tossed four times, and a person win Re 1 for each head and lose Rs 1.50 for each tail that turns up.
From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.
If 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when, the digits are repeated?
A bag contains 5 red, 6 white and 7 black balls. Two balls are drawn at random. What is the probability that both balls are red or both are black?
If a letter is chosen at random from the English alphabet, find the probability that the letter is a vowel .
In a lottery, a person chooses six different numbers at random from 1 to 20, and if these six numbers match with six number already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game?
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (i) | 0.1 | 0.01 | 0.05 | 0.03 | 0.01 | 0.2 | 0.6 |
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (ii) |
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
In a single throw of three dice, find the probability of getting the same number on all the three dice.
A box contains 100 bulbs, 20 of which are defective. 10 bulbs are selected for inspection. Find the probability that all 10 are good
A box contains 100 bulbs, 20 of which are defective. 10 bulbs are selected for inspection. Find the probability that none is defective
Two dice are thrown together. The probability that neither they show equal digits nor the sum of their digits is 9 will be
Three squares of chessboard are selected at random. The probability of getting 2 squares of one colour and other of a different colour is ______.
One mapping (function) is selected at random from all the mappings of the set A = {1, 2, 3, ..., n} into itself. The probability that the mapping selected is one to one is ______.
Six new employees, two of whom are married to each other, are to be assigned six desks that are lined up in a row. If the assignment of employees to desks is made randomly, what is the probability that the married couple will have nonadjacent desks?
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine P(B ∩ C)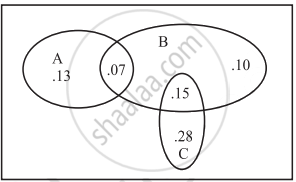
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that all the three balls are red
If the letters of the word ASSASSINATION are arranged at random. Find the probability that four S’s come consecutively in the word
While shuffling a pack of 52 playing cards, 2 are accidentally dropped. Find the probability that the missing cards to be of different colours ______.
A single letter is selected at random from the word ‘PROBABILITY’. The probability that it is a vowel is ______.
If the probabilities for A to fail in an examination is 0.2 and that for B is 0.3, then the probability that either A or B fails is ______.
The probability that a student will pass his examination is 0.73, the probability of the student getting a compartment is 0.13, and the probability that the student will either pass or get compartment is 0.96.
The sum of probabilities of two students getting distinction in their final examinations is 1.2
| C1 Probability |
C2 Written Description |
| (a) 0.95 | (i) An incorrect assignment |
| (b) 0.02 | (ii) No chance of happening |
| (c) – 0.3 | (iii) As much chance of happening as not |
| (d) 0.5 | (iv) Very likely to happen |
| (e) 0 | (v) Very little chance of happening |
