Advertisements
Advertisements
Question
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Advertisements
Solution
(i) Since number of sides in the pentagon = 5
Each exterior angle = `360/5 = 72^circ`
∠BAE = 180° – 72°= 108°
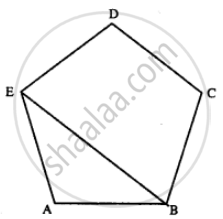
(ii) In Δ ABE, AB = AE
∴ ∠ABE = ∠AEB
But ∠BAE + ∠ABE + ∠ AEB = 180°
∴ 108° + 2 ∠ABE = 180° – 108° = 72°
⇒ ∠ABE = 36°
(iii) Since ∠AED = 108° ...[∵ each interior angle = 108°]
⇒ ∠AEB = 36°
⇒ ∠BED = 108° – 36° = 72°
APPEARS IN
RELATED QUESTIONS
Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.
The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :
(i) measure of each interior angle ;
(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
The ratio between the interior angle and the exterior angle of a regular polygon is 2: 1. Find:
(i) each exterior angle of the polygon ;
(ii) number of sides in the polygon.
AB, BC and CD are three consecutive sides of a regular polygon. If angle BAC = 20° ; find :
(i) its each interior angle,
(ii) its each exterior angle
(iii) the number of sides in the polygon.
If the difference between the exterior angle of a 'n' sided regular polygon and an (n + 1) sided regular polygon is 12°, find the value of n.
Calculate the number of sides of a regular polygon, if: its interior angle is five times its exterior angle.
Is it possible to have a regular polygon whose interior angle is: 155°
What is the measure of each interior angle of a regular hexagon?
Which formula correctly represents the sum of interior angles of an n-sided polygon?
