Advertisements
Advertisements
Question
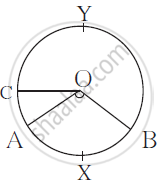
In the following figure ‘O’ is the centre of the circle.
∠AOB = 1100, m(arc AC) = 450.
Use the information and fill in the boxes with proper numbers.
(i) m(arcAXB) =
(ii)m(arcCAB) =
(iv)∠COB =
(iv)m(arcAYB) =
Solution
From the figure,
(i) m(arc AXB) = 110°
(ii) m(arc CAB) = 155°
(iii) ∠COB = 155°
(iv) m(arc AYB) = 250°
APPEARS IN
RELATED QUESTIONS
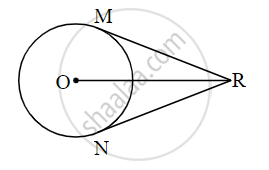
In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
- What is the length of each tangent segment?
- What is the measure of ∠MRO?
- What is the measure of ∠MRN?

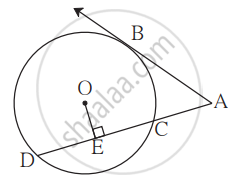
In the given figure, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find (1) AD (2) DC (3) DE.
Four alternative answers for the following question is given. Choose the correct alternative.
Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
In the given figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that ▢ABOC is a square. 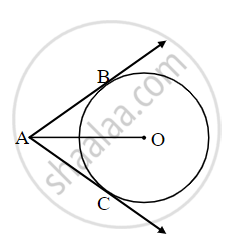
Proof: Draw segment OB and OC.
l(AB) = r ......[Given] (I)
AB = AC ......[`square`] (II)
But OB = OC = r ......[`square`] (III)
From (i), (ii) and (iii)
AB = `square` = OB = OC = r
∴ Quadrilateral ABOC is `square`
Similarly, ∠OBA = `square` ......[Tangent Theorem]
If one angle of `square` is right angle, then it is a square.
∴ Quadrilateral ABOC is a square.
The perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
Prove the following theorem:
Tangent segments drawn from an external point to the circle are congruent.
Segment DP and segment DQ are tangent segments to the circle with center A. If DP = 7 cm. So find the length of the segment DQ.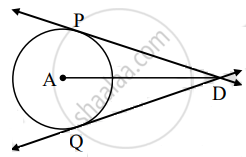
The chords corresponding to congruent arcs of a circle are congruent. Prove the theorem by completing following activity.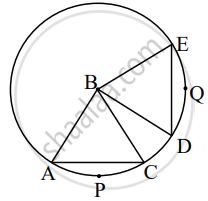
Given: In a circle with centre B
arc APC ≅ arc DQE
To Prove: Chord AC ≅ chord DE
Proof: In ΔABC and ΔDBE,
side AB ≅ side DB ......`square`
side BC ≅ side `square` .....`square`
∠ABC ≅ ∠DBE ......[Measure of congruent arcs]
∆ABC ≅ ∆DBE ......`square`
Tangent segments drawn from an external point to a circle are congruent, prove this theorem. Complete the following activity.
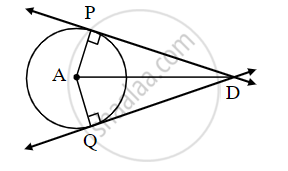
Given: `square`
To Prove: `square`
Proof: Draw radius AP and radius AQ and complete the following proof of the theorem.
In ∆PAD and ∆QAD,
seg PA ≅ `square` .....[Radii of the same circle]
seg AD ≅ seg AD ......[`square`]
∠APD ≅ ∠AQD = 90° .....[Tangent theorem]
∴ ∆PAD ≅ ∆QAD ....[`square`]
∴ seg DP ≅ seg DQ .....[`square`]
In the adjoining figure, O is the center of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
(i) What is the length of each tangent segment?
(ii) What is the measure of ∠MRO?
(iii) What is the measure of ∠MRN?
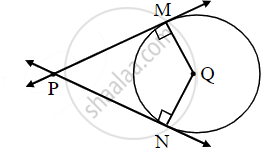
In the adjoining figure circle with Centre, Q touches the sides of ∠MPN at M and N. If ∠MPN = 40°, find measure of ∠MQN.
If AB and CD are the common tangents in the circles of two unequal (different) radii, then show that seg AB ≅ seg CD.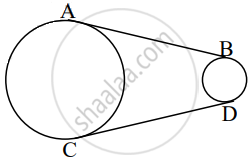
Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity.

Proof: In ∆RMO and ∆RNO,
∠RMO ≅ ∠RNO = 90° ......[`square`]
hypt OR ≅ hypt OR ......[`square`]
seg OM ≅ seg `square` ......[Radii of the same circle]
∴ ∆RMO ≅ ∆RNO ......[`square`]
∠MOR ≅ ∠NOR
Similairy ∠MRO ≅ `square` ......[`square`]
Prove that, tangent segments drawn from an external point to the circle are congruent.
In a parallelogram ABCD, ∠B = 105°. Determine the measure of ∠A and ∠D.

A circle touches side BC at point P of the ΔABC, from outside of the triangle. Further extended lines AC and AB are tangents to the circle at N and M respectively. Prove that : AM = `1/2` (Perimeter of ΔABC)
