Advertisements
Advertisements
Question
In parallelogram ABCD, its diagonals intersect at point O. If OA = 6 cm and OB = 7.5 cm, find the length of AC and BD.

Solution
∵ When diagonals AC and BD intersect each other at point O,
then OA = OC = `1/2` AC
and OB = OD = `1/2` BD
∴ OA = `1/2 xx` AC ⇒ AC = 2 × OA
⇒ AC = 2 × 6 cm = 12 cm,
and OB = `1/2 xx "BD"` ⇒ BD = 2 × OB
⇒ BD = 2 × 7.5 cm ⇒ BD = 15 cm
APPEARS IN
RELATED QUESTIONS
How many diagonals does following have?
A regular hexagon
In a quadrilateral, define of the following Vertices .
In a quadrilateral, define of the following Angles .
Complete of the following, so as to make a true statement:
A quadrilateral has ....... sides.
Complete of the following, so as to make a true statement:
A quadrilateral has .... diagonals.
Complete of the following, so as to make a true statement:
The sum of the angles of a quiadrilateral is .... right angles.
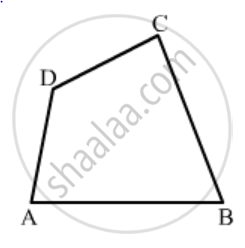
In Fig. 16.19, ABCD is a quadrilateral.
Name a pair of adjacent angles.
The angles of a quadrilateral are 110°, 72°, 55° and x°. Find the value of x.
A quadrilateral has three acute angles each measures 80°. What is the measure of the fourth angle?
If the sum of the two angles of a quadrilateral is 180°. What is the sum of the remaining two angles?
Complete the following statement by means of one of those given in brackets against each:
If in a quadrilateral only one pair of opposite sides are parallel, the quadrilateral is ................
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
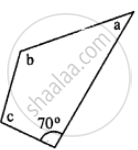
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
The angles A, B, C and D of a quadrilateral are in the ratio 2 : 3 : 2 : 3. Show this quadrilateral is a parallelogram.
The angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°. Find the angles.
Calculate the measure of each angle of a nonagon.
In the quadrilateral ABCD, AB = BC and AD = DC Measure of ∠BCD is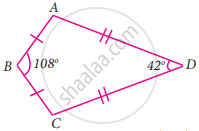
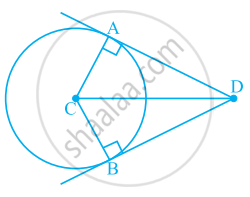
What conclusion can be drawn from part of given figure, if BD bisects ∠ABC?
What conclusion can be drawn from part of given figure, if DC is the bisector of ∠ADB, CA ⊥ DA and CB ⊥ DB?