Advertisements
Advertisements
Question
Let A = [1, 2] and B = [3, 4]. Find the total number of relation from A into B.
Solution
We have:
A = {1, 2} and B = {3, 4}
Now,
There are 2n relations from A to B, where n is the number of elements in their Cartesian product.
∴ Number of relations from A to B is 24 = 16.
APPEARS IN
RELATED QUESTIONS
Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
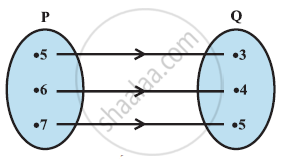
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
Find the inverse relation R−1 in each of the cases:
(ii) R = {(x, y), : x, y ∈ N, x + 2y = 8}
Determine the domain and range of the relations:
(i) R = {(a, b) : a ∈ N, a < 5, b = 4}
Define a relation R on the set N of natural number by R = {(x, y) : y = x + 5, x is a natural number less than 4, x, y ∈ N}. Depict this relationship using (i) roster form (ii) an arrow diagram. Write down the domain and range or R.
The adjacent figure shows a relationship between the sets P and Q. Write this relation in (i) set builder form (ii) roster form. What is its domain and range?
For the relation R1 defined on R by the rule (a, b) ∈ R1 ⇔ 1 + ab > 0. Prove that: (a, b) ∈ R1 and (b , c) ∈ R1 ⇒ (a, c) ∈ R1 is not true for all a, b, c ∈ R.
If n(A) = 3, n(B) = 4, then write n(A × A × B).
Let R = [(x, y) : x, y ∈ Z, y = 2x − 4]. If (a, -2) and (4, b2) ∈ R, then write the values of a and b.
If R = [(x, y) : x, y ∈ W, 2x + y = 8], then write the domain and range of R.
Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, write A and B
If A = {1, 2, 4}, B = {2, 4, 5}, C = {2, 5}, then (A − B) × (B − C) is
Let R be a relation from a set A to a set B, then
If R is a relation from a finite set A having m elements of a finite set B having n elements, then the number of relations from A to B is
Let A = {6, 8} and B = {1, 3, 5}
Show that R1 = {(a, b)/a ∈ A, b ∈ B, a − b is an even number} is a null relation. R2 = {(a, b)/a ∈ A, b ∈ B, a + b is odd number} is an universal relation
Write the relation in the Roster Form. State its domain and range
R5 = {(x, y)/x + y = 3, x, y∈ {0, 1, 2, 3}
Write the relation in the Roster Form. State its domain and range
R8 = {(a, b)/b = a + 2, a ∈ z, 0 < a < 5}
Select the correct answer from given alternative.
A relation between A and B is
Answer the following:
Determine the domain and range of the following relation.
R = {(a, b)/a ∈ N, a < 5, b = 4}
Answer the following:
Find R : A → A when A = {1, 2, 3, 4} such that R = {(a, b)/|a − b| ≥ 0}
Answer the following:
R = {1, 2, 3} → {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} Check if R is reflexive
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, the following is relation from A to B?
R2 = {(–1, 1)}
Let A = {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f : A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f
Discuss the following relation for reflexivity, symmetricity and transitivity:
Let A be the set consisting of all the members of a family. The relation R defined by “aRb if a is not a sister of b”
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it transitive
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it equivalence
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it transitive
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is symmetric
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is transitive
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is equivalence
Choose the correct alternative:
The relation R defined on a set A = {0, −1, 1, 2} by xRy if |x2 + y2| ≤ 2, then which one of the following is true?
Choose the correct alternative:
Let f : R → R be defined by f(x) = 1 − |x|. Then the range of f is
Is the following relation a function? Justify your answer
R2 = {(x, |x |) | x is a real number}
Is the given relation a function? Give reasons for your answer.
h = {(4, 6), (3, 9), (– 11, 6), (3, 11)}
Let n(A) = m, and n(B) = n. Then the total number of non-empty relations that can be defined from A to B is ______.
A relation on the set A = {x : |x| < 3, x ∈ Z}, where Z is the set of integers is defined by R = {(x, y) : y = |x| ≠ –1}. Then the number of elements in the power set of R is ______.
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Is the following true?
f is a function from A to B
Justify your answer in case.
