Advertisements
Advertisements
Question
Obtain Bohr’s quantisation condition for angular momentum of electron orbiting in nth orbit in hydrogen atom on the basis of the wave picture of an electron using de Broglie hypothesis.
Solution 1
`n lambda = 2 pi r`
But ` lambda = n/(mv) `( By De Broglie)
`(n lambda) /(mv) = 2 pi r`
` therefore (lambda n) /(2 pi ) = mvr ` (mvr = L)
` therefore L = (lambda n)/(2 pi)`
Solution 2
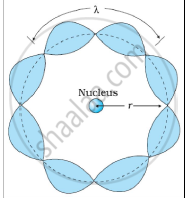
Bohr's second postulate states that the angular momentum of an electron has only those values that are integral multiples of `"h"/(2pi)` He thought that the motion of electrons within an atom is associated with the standing wave along the orbit as shown.
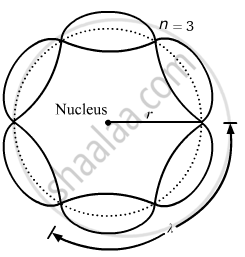
About standing waves in stretched strings, we know that only those waves survive for which the distances traveled in the round trip between the ends are integral multiples of the wavelength. Similarly, for an electron moving in the nth orbit of radius rn, the distance traveled in one trip is 2πrn, which should be an integral multiple of the wavelength.
2πrn = nλ (where n= 1, 2, 3, 4 etc)
By de-Broglie hypothesis, we have:
`lambda = "h"/"p" = "h"/("mv"_"n")`
Substituting the value of λ in the above expression, we get:
`2pi"r"_"n" = "n" "h"/"mv"_"n"`
⇒ `"mv"_"n""r"_"n" = "n" "h"/(2pi)`
Angular momentum `= "L" = "n" "h"/(2pi)`
RELATED QUESTIONS
Calculate the radius of second Bohr orbit in hydrogen atom from the given data.
Mass of electron = 9.1 x 10-31kg
Charge on the electron = 1.6 x 10-19 C
Planck’s constant = 6.63 x 10-34 J-s.
Permittivity of free space = 8.85 x 10-12 C2/Nm2
Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Using Bohr's postulates, derive the expression for the total energy of the electron in the stationary states of the hydrogen atom ?
According to the Bohr theory of H-atom, the speed of the electron, its energy and the radius of its orbit varies with the principal quantum number n, respectively, as:
The wavelength of the first time line of Ballmer series is 6563 A°. The Rydberg constant for hydrogen is about:-
The angular momentum of electron in nth orbit is given by
The wavelength in Å of the photon that is emitted when an electron in Bohr orbit with n = 2 returns to orbit with n = 1 in H atom is ______ Å. The ionisation potential of the ground state of the H-atom is 2.17 × 10−11 erg.
Find the ratio of energies of photons produced due to transition of an election of hydrogen atom from its (i) second permitted energy level to the first level. and (ii) the highest permitted energy level to the first permitted level.
According to Bohr atom model, in which of the following transitions will the frequency be maximum?
An electron in a hydrogen atom has an energy of -3.4 eV. The difference between its kinetic and potential energy is ______.
