Advertisements
Advertisements
Question
Find the number of molecules in 1 cm3 of an ideal gas at 0°C and at a pressure of 10−5mm of mercury.
Use R = 8.31 J K-1 mol-1
Solution
Given:
Volume of ideal gas, V = 1 cm3 = 10-6 m3
Temperature of ideal gas, T = 0 °C = 273 K
Pressure of mercury, P = 10−8 m of Hg
Density of ideal gas, ρ = 13600 kgm-3
Pressure \[\left( P \right)\] is given by
P = ρgh
Here,
ρ = density of ideal gas
g = acceleration due to gravity,
Using the ideal gas equation, we get
\[n = \frac{PV}{RT}\]
\[ \Rightarrow n = \frac{\rho gh \times V}{RT}\]
\[ \Rightarrow n = \frac{13600 \times 9 . 8 \times {10}^{- 8} \times {10}^{- 6}}{8 . 31 \times 273}\]
\[ \Rightarrow n = 5 . 87 \times {10}^{- 13} \]
Number of molecules = N × n
= 6.023 × 1023×5.874 × 10−13
= 35.384 × 1010
= 3.538 × 1011
APPEARS IN
RELATED QUESTIONS
The energy of a given sample of an ideal gas depends only on its
Keeping the number of moles, volume and temperature the same, which of the following are the same for all ideal gases?
The average momentum of a molecule in a sample of an ideal gas depends on
Consider the quantity \[\frac{MkT}{pV}\] of an ideal gas where M is the mass of the gas. It depends on the
Calculate the volume of 1 mole of an ideal gas at STP.
A vessel containing one mole of a monatomic ideal gas (molecular weight = 20 g mol−1) is moving on a floor at a speed of 50 m s−1. The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas, find the rise in its temperature.
An amount Q of heat is added to a monatomic ideal gas in a process in which the gas performs a work Q/2 on its surrounding. Find the molar heat capacity for the process
An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p = kV. Show that the molar heat capacity of the gas for the process is given by `"C" ="C"_"v" +"R"/2.`
Two ideal gases have the same value of Cp / Cv = γ. What will be the value of this ratio for a mixture of the two gases in the ratio 1 : 2?
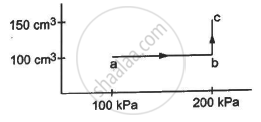
An ideal gas (γ = 1.67) is taken through the process abc shown in the figure. The temperature at point a is 300 K. Calculate (a) the temperatures at b and c (b) the work done in the process (c) the amount of heat supplied in the path ab and in the path bcand (d) the change in the internal energy of the gas in the process.
The volume of an ideal gas (γ = 1.5) is changed adiabatically from 4.00 litres to 3.00 litres. Find the ratio of (a) the final pressure to the initial pressure and (b) the final temperature to the initial temperature.
Two samples A and B, of the same gas have equal volumes and pressures. The gas in sample A is expanded isothermally to double its volume and the gas in B is expanded adiabatically to double its volume. If the work done by the gas is the same for the two cases, show that γ satisfies the equation 1 − 21−γ = (γ − 1) ln2.
1 litre of an ideal gas (γ = 1.5) at 300 K is suddenly compressed to half its original volume. (a) Find the ratio of the final pressure to the initial pressure. (b) If the original pressure is 100 kPa, find the work done by the gas in the process. (c) What is the change in internal energy? (d) What is the final temperature? (e) The gas is now cooled to 300 K keeping its pressure constant. Calculate the work done during the process. (f) The gas is now expanded isothermally to achieve its original volume of 1 litre. Calculate the work done by the gas. (g) Calculate the total work done in the cycle.
Figure shows a cylindrical tube with adiabatic walls and fitted with an adiabatic separator. The separator can be slid into the tube by an external mechanism. An ideal gas (γ = 1.5) is injected in the two sides at equal pressures and temperatures. The separator remains in equilibrium at the middle. It is now slid to a position where it divides the tube in the ratio 1 : 3. Find the ratio of the temperatures in the two parts of the vessel.

The figure shows an adiabatic cylindrical tube of volume V0 divided in two parts by a frictionless adiabatic separator. Initially, the separator is kept in the middle, an ideal gas at pressure p1 and temperature T1 is injected into the left part and another ideal gas at pressure p2 and temperature T2 is injected into the right part. Cp/Cv = γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

A cubic vessel (with faces horizontal + vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of 500 ms–1 in vertical direction. The pressure of the gas inside the vessel as observed by us on the ground ______.
ABCDEFGH is a hollow cube made of an insulator (Figure). Face ABCD has positive charge on it. Inside the cube, we have ionized hydrogen. The usual kinetic theory expression for pressure ______.
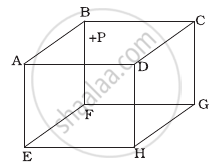
- will be valid.
- will not be valid since the ions would experience forces other than due to collisions with the walls.
- will not be valid since collisions with walls would not be elastic.
- will not be valid because isotropy is lost.
Diatomic molecules like hydrogen have energies due to both translational as well as rotational motion. From the equation in kinetic theory `pV = 2/3` E, E is ______.
- the total energy per unit volume.
- only the translational part of energy because rotational energy is very small compared to the translational energy.
- only the translational part of the energy because during collisions with the wall pressure relates to change in linear momentum.
- the translational part of the energy because rotational energies of molecules can be of either sign and its average over all the molecules is zero.
We have 0.5 g of hydrogen gas in a cubic chamber of size 3 cm kept at NTP. The gas in the chamber is compressed keeping the temperature constant till a final pressure of 100 atm. Is one justified in assuming the ideal gas law, in the final state?
(Hydrogen molecules can be consider as spheres of radius 1 Å).
