Advertisements
Advertisements
Question
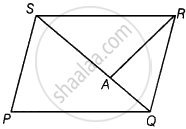
PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ASR = 90 cm2.
Options
True
False
Solution
This statement is False.
Explanation:
Given, area of parallelogram PQRS = 180 cm2 and QS is its diagonal which divides it into two triangles of equal area.
APPEARS IN
RELATED QUESTIONS
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 1/4ar (ABC).
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 1/4ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
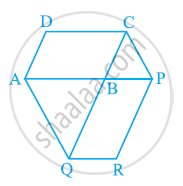
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that
ar (ABCD) = ar (PBQR).
[Hint: Join AC and PQ. Now compare area (ACQ) and area (APQ)]
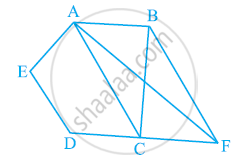
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
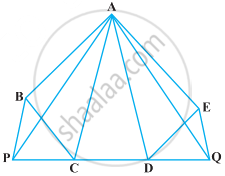
In the given figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar(PRQ) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
The area of the parallelogram ABCD is 90 cm2 (see figure). Find ar (ΔABD)
A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC)
In the following figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ)