Advertisements
Advertisements
Question
Prove that the perpendicular drawn from the point (4, 1) on the join of (2, −1) and (6, 5) divides it in the ratio 5 : 8.
Advertisements
Solution
Let PD be the perpendicular drawn from P (4, 1) on the line joining the points \[A\left( 2, - 1 \right) \text { and } B\left( 6, 5 \right)\].
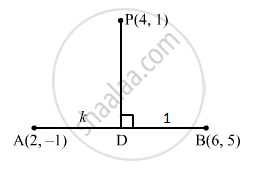
Let m be the slope of PD.
\[\therefore m \times \text { Slope of }AB = - 1\]
\[ \Rightarrow m \times \left( \frac{5 + 1}{6 - 2} \right) = - 1\]
\[ \Rightarrow m \times \frac{6}{4} = - 1\]
\[ \Rightarrow m \times \frac{3}{2} = - 1\]
\[ \Rightarrow m = - \frac{2}{3}\]
Thus, the equation of line PD passing through P (4, 1) and having slope \[- \frac{2}{3}\] is
\[y - 1 = - \frac{2}{3}\left( x - 4 \right)\]
\[ \Rightarrow 3y - 3 = - 2x + 8\]
\[ \Rightarrow 2x + 3y - 11 = 0\]
Let D divide the line AB in the ratio k : 1
Then, the coordinates of D are \[\left( \frac{6k + 2}{k + 1}, \frac{5k - 1}{k + 1} \right)\].
Since, D lies on AB whose equation is \[2x + 3y - 11 = 0\]
Therefore, it satisfy the equation.
\[\therefore 2\left( \frac{6k + 2}{k + 1} \right) + 3\left( \frac{5k - 1}{k + 1} \right) - 11 = 0\]
\[ \Rightarrow 12k + 4 + 15k - 3 - 11k - 11 = 0\]
\[ \Rightarrow 16k = 10\]
\[ \Rightarrow k = \frac{5}{8}\]
Hence, the perpendicular drawn from the point (4, 1) on the line joining the points (2, −1) and (6, 5) divides it in the ratio 5 : 8
APPEARS IN
RELATED QUESTIONS
Find the equation of the line perpendicular to x-axis and having intercept − 2 on x-axis.
Draw the lines x = − 3, x = 2, y = − 2, y = 3 and write the coordinates of the vertices of the square so formed.
Find the equation of a line equidistant from the lines y = 10 and y = − 2.
Find the equation of the straight line passing through the point (6, 2) and having slope − 3.
Find the equation of the straight line which passes through the point (1,2) and makes such an angle with the positive direction of x-axis whose sine is \[\frac{3}{5}\].
Find the equation of the straight line which divides the join of the points (2, 3) and (−5, 8) in the ratio 3 : 4 and is also perpendicular to it.
Find the equations to the altitudes of the triangle whose angular points are A (2, −2), B (1, 1) and C (−1, 0).
Find the equations of the medians of a triangle, the coordinates of whose vertices are (−1, 6), (−3, −9) and (5, −8).
By using the concept of equation of a line, prove that the three points (−2, −2), (8, 2) and (3, 0) are collinear.
Find the equations to the straight lines which go through the origin and trisect the portion of the straight line 3 x + y = 12 which is intercepted between the axes of coordinates.
Find the equation to the straight line cutting off intercepts − 5 and 6 from the axes.
Find the equation to the straight line which passes through the point (5, 6) and has intercepts on the axes
(i) equal in magnitude and both positive,
(ii) equal in magnitude but opposite in sign.
Find the equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
Find the equation of the straight line which passes through the point P (2, 6) and cuts the coordinate axes at the point A and B respectively so that \[\frac{AP}{BP} = \frac{2}{3}\] .
A line is such that its segment between the straight lines 5x − y − 4 = 0 and 3x + 4y − 4 = 0 is bisected at the point (1, 5). Obtain its equation.
If the straight line \[\frac{x}{a} + \frac{y}{b} = 1\] passes through the point of intersection of the lines x + y = 3 and 2x − 3y = 1 and is parallel to x − y − 6 = 0, find a and b.
Find the equation of a line passing through (3, −2) and perpendicular to the line x − 3y + 5 = 0.
Find the equation of the straight line through the point (α, β) and perpendicular to the line lx + my + n = 0.
The line 2x + 3y = 12 meets the x-axis at A and y-axis at B. The line through (5, 5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
Find the length of the perpendicular from the point (4, −7) to the line joining the origin and the point of intersection of the lines 2x − 3y + 14 = 0 and 5x + 4y − 7 = 0.
Two sides of an isosceles triangle are given by the equations 7x − y + 3 = 0 and x + y − 3 = 0 and its third side passes through the point (1, −10). Determine the equation of the third side.
Prove that the family of lines represented by x (1 + λ) + y (2 − λ) + 5 = 0, λ being arbitrary, pass through a fixed point. Also, find the fixed point.
Show that the straight lines given by (2 + k) x + (1 + k) y = 5 + 7k for different values of k pass through a fixed point. Also, find that point.
Find the equation of the straight line passing through the point of intersection of 2x + y − 1 = 0 and x + 3y − 2 = 0 and making with the coordinate axes a triangle of area \[\frac{3}{8}\] sq. units.
Write the area of the triangle formed by the coordinate axes and the line (sec θ − tan θ) x + (sec θ + tan θ) y = 2.
If the diagonals of the quadrilateral formed by the lines l1x + m1y + n1 = 0, l2x + m2y + n2 = 0, l1x + m1y + n1' = 0 and l2x + m2y + n2' = 0 are perpendicular, then write the value of l12 − l22 + m12 − m22.
If a, b, c are in G.P. write the area of the triangle formed by the line ax + by + c = 0 with the coordinates axes.
A line passes through the point (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is
If a + b + c = 0, then the family of lines 3ax + by + 2c = 0 pass through fixed point
A straight line moves so that the sum of the reciprocals of its intercepts made on axes is constant. Show that the line passes through a fixed point.
The equation of the line passing through the point (1, 2) and perpendicular to the line x + y + 1 = 0 is ______.
If a, b, c are in A.P., then the straight lines ax + by + c = 0 will always pass through ______.
Equation of the line passing through the point (a cos3θ, a sin3θ) and perpendicular to the line x sec θ + y cosec θ = a is x cos θ – y sin θ = a sin 2θ.
The straight line 5x + 4y = 0 passes through the point of intersection of the straight lines x + 2y – 10 = 0 and 2x + y + 5 = 0.
