Advertisements
Advertisements
Question
Represent `sqrt9.3` on the number line.
Solution
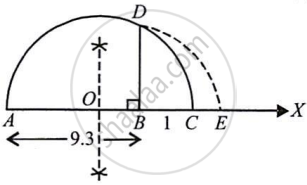
Draw a line segment AB = 9.3 units and extend it to C such that BC = 1 unit.
Find the midpoint of AC and mark it as O.
Draw a semicircle with O as the centre and AO as the radius.
Draw BD ⊥ AC.
Draw an arc with B as the centre and BD and produce radius AC at E such that BE = BD = `sqrt9.3` units.
APPEARS IN
RELATED QUESTIONS
Simplify the following expressions:
`(11 + sqrt11)(11 - sqrt11)`
Simplify the following expressions:
`(sqrt8 - sqrt2)(sqrt8 + sqrt2)`
Express each one of the following with rational denominator:
`(b^2)/(sqrt(a^2 + b^2) + a)`
Simplify:
`(5 + sqrt3)/(5 - sqrt3) + (5 - sqrt3)/(5 + sqrt3)`
Simplify:
`2/(sqrt5 + sqrt3) + 1/(sqrt3 + sqrt2) - 3/(sqrt5 + sqrt2)`
Write the reciprocal of \[5 + \sqrt{2}\].
If\[\frac{\sqrt{3} - 1}{\sqrt{3} + 1} = x + y\sqrt{3},\] find the values of x and y.
Write the rationalisation factor of \[\sqrt{5} - 2\].
If \[\frac{\sqrt{3 - 1}}{\sqrt{3} + 1}\] =\[a - b\sqrt{3}\] then
Rationalise the denominator of the following:
`(sqrt(3) + sqrt(2))/(sqrt(3) - sqrt(2))`
