Advertisements
Advertisements
Question
Solve the following equation for A, if 2cos2A = 1
Solution
2 cos 2 A = 1
cos 2 A = `(1)/(2)`
cos 2 A = cos 60°
2A = 60°
A = 30°
APPEARS IN
RELATED QUESTIONS
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
Use the given figure to find:
(i) tan θ°
(ii) θ°
(iii) sin2θ° - cos2θ°
(iv) Use sin θ° to find the value of x.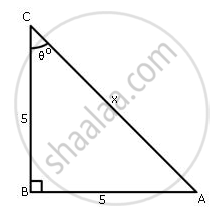
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
If sin 3A = 1 and 0 < A < 90°, find cos 2A
Solve for x : 3 tan2 (2x - 20°) = 1
If A = B = 60°, verify that: tan(A - B) = `(tan"A" - tan"B")/(1 + tan"A" tan"B"")`
Evaluate the following: `(2sin28°)/(cos62°) + (3cot49°)/(tan41°)`
If sec2θ = cosec3θ, find the value of θ if it is known that both 2θ and 3θ are acute angles.
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
