Advertisements
Advertisements
Question
The rate constant of a first order reaction increases from 2 × 10−2 to 4 × 10−2 when the temperature changes from 300 K to 310 K. Calculate the energy of activation (Ea).
(log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021)
Solution
According to the Arrhenius equation,
k=Ae(−Ea/RT)
From this, we get
`"log"k_2/k_1=E_a/(2.303R)((T_2-T_1)/(T_1T_2))`
We are given that
Initial temperature, T1=300 K
Final temperature, T2=310 K
Rate constant at initial temperature, k1=2×10−2
Rate constant at final temperature, k2=4×10−2
Gas constant, R=8.314 J K−1 mol−1
Substituting the values, we get
`"log"((4xx10^(-2))/(2xx10^(-2)))=E_a/(2.303xx8.314)((310-300)/(300xx310))`
`therefore " activation energy of the reaction, "E_a=(log2xx2.303xx8.314xx300xx310)/10`
`=535985.94" J mol"^(-1)`
`=535.98" kJ mol"^(-1)`
RELATED QUESTIONS
Explain a graphical method to determine activation energy of a reaction.
What is the effect of adding a catalyst on Activation energy (Ea)
The decomposition of a hydrocarbon has value of rate constant as 2.5×104s-1 At 27° what temperature would rate constant be 7.5×104 × 3 s-1if energy of activation is 19.147 × 103 J mol-1 ?
Predict the main product of the following reactions: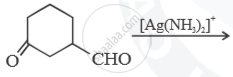
The chemical reaction in which reactants require high amount of activation energy are generally ____________.
During decomposition of an activated complex:
(i) energy is always released
(ii) energy is always absorbed
(iii) energy does not change
(iv) reactants may be formed
Which of the following statements are in accordance with the Arrhenius equation?
(i) Rate of a reaction increases with increase in temperature.
(ii) Rate of a reaction increases with decrease in activation energy.
(iii) Rate constant decreases exponentially with increase in temperature.
(iv) Rate of reaction decreases with decrease in activation energy.
The reaction between \[\ce{H2(g)}\] and \[\ce{O2(g)}\] is highly feasible yet allowing the gases to stand at room temperature in the same vessel does not lead to the formation of water. Explain.
Oxygen is available in plenty in air yet fuels do not burn by themselves at room temperature. Explain.
The rate constant for a reaction is 1.5 × 10–7 sec–1 at 50°C. What is the value of activation energy?
