Advertisements
Advertisements
Question
The area of the triangle formed by the points A(2,0) B(6,0) and C(4,6) is
Options
24 sq. units
12 sq. units
10 sq. units
none of these
Solution
Given that points A(2,0), B(6,0) and C(4 ,6) form a triangle which is shown in the figure. We are asked to find the area of the triangle ΔABC.
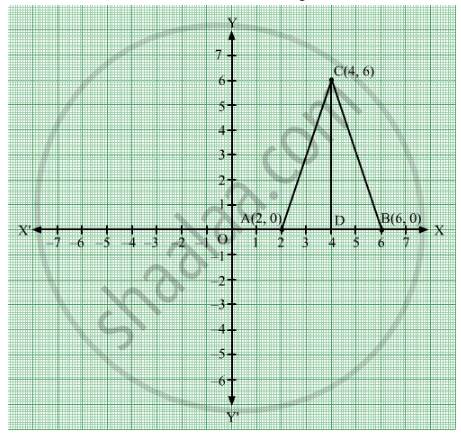
Given that
OA = 2
and OB = 6
Hence
\[\text { AB = OB - OA}\]
\[ = 6 - 2\]
\[ = 4\]
CD = 6
By using formula,
\[∆\text { ABC }= \frac{1}{2} \times \text { AB} \times \text{CD}\]
\[ = \frac{1}{2} \times 4 \times 6\]
\[ = 12 \text { sq units} \]
APPEARS IN
RELATED QUESTIONS
Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when A coincides with the origin and AB and AD are along OX and OY respectively.
If two opposite vertices of a square are (5, 4) and (1, −6), find the coordinates of its remaining two vertices.
In what ratio is the line segment joining the points (-2,-3) and (3, 7) divided by the y-axis? Also, find the coordinates of the point of division.
In what ratio is the line segment joining the points A(-2, -3) and B(3,7) divided by the yaxis? Also, find the coordinates of the point of division.
Find the ratio in which the point (-1, y) lying on the line segment joining points A(-3, 10) and (6, -8) divides it. Also, find the value of y.
Find the coordinates of the centre of the circle passing through the points P(6, –6), Q(3, –7) and R (3, 3).
Find the value of k, if the points A (8, 1) B(3, −4) and C(2, k) are collinear.
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k
Abscissa of a point is positive in ______.
Find the coordinates of the point whose ordinate is – 4 and which lies on y-axis.
