Advertisements
Advertisements
Question
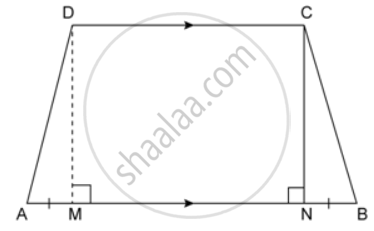
The cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure; also given that:
AM = BN; AB = 7 m; CD = 5 m. The height of the tunnel is 2.4 m. The tunnel is 40 m long. Calculate:
(i) The cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m2 (sq. meter).
(ii) The cost of paving the floor at the rate of Rs. 18 per m2.
Solution
The cross-section of a tunnel is of the trapezium-shaped ABCD in which AB = 7 m, CD = 5 m and AM = BN. The height is 2.4 m and its length is 40 m.
(i) AM = BN =`( 7 - 5 )/( 2 )= ( 2 )/( 2 ) =1"m"`
∴ In ΔADM,
AD2 = AM2 + DM2 ...[ Using Pythagoras theorem ]
= 12 + (2 . 4)2
= 1 + 5.76
= `sqrt6.76`
= 2.6
AD = 2.6 m
Perimeter of the cross-section of the tunnel = ( 7 + 2.6 + 2.6 + 5 ) m = 17.2 m
Length = 40 m
∴ The internal surface area of the tunnel ( except the floor )
= ( 17.2 × 40 - 40 × 7) m2
= ( 688 - 280 ) m2
= 408 m2
Rate of painting = Rs. 5 per m2
Hence, total cost of painting = Rs. 5 × 408 = Rs. 2040
(ii) Area of floor of tunnel = l × b = 40 × 7 = 280 m2
Rate of cost of paving = Rs. 18 per m2
Total cost = 280 × 18 = Rs. 5040
APPEARS IN
RELATED QUESTIONS
The following figure shows a closed victory-stand whose dimensions are given in cm.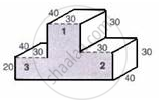
Find the volume and the surface area of the victory stand.
A rectangular water-tank measuring 80 cm x 60 cm is filled form a pipe of cross-sectional area 1.5 cm2, the water emerging at 3.2 m/s. How long does it take to fill the tank?
A school auditorium is 40 m long, 30 m broad and 12 m high. If each student requires 1.2 m2 of the floor area; find the maximum number of students that can be accommodated in this auditorium. Also, find the volume of air available in the auditorium, for each student.
A rectangular field is 112 m long and 62 m broad. A cubical tank of edge 6 m is dug at each of the four corners of the field and the earth so removed is evenly spread on the remaining field. Find the rise in level.
The cross section of a piece of metal 2 m in length
is shown. Calculate the volume of the piece of metal.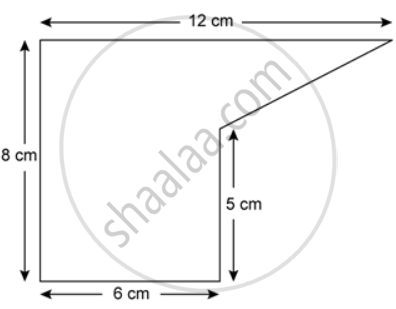
The figure represents the cross section of a swimming pool 10 m broad, 2 m deep at one end, 3 m deep at the other end. Calculate the volume of water it will hold when full, given that its length is 40 m.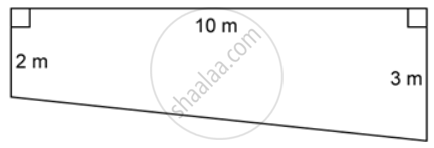
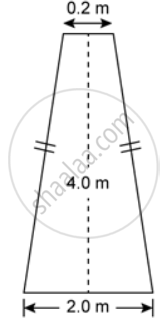
The figure shows the cross section of 0.2 m a concrete wall to be constructed. It is 0.2 m wide at the top, 2.0 m wide at the bottom and its height is 4.0 m, and its length is 40 m. Calculate the volume of the concrete in the wall
The cross section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m, CD = 3 m The height of a tunnel is 2.4 m. The tunnel is 5.4 m long. Calculate the cost of flooring at the rate of Rs.2. 5 per m2.
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.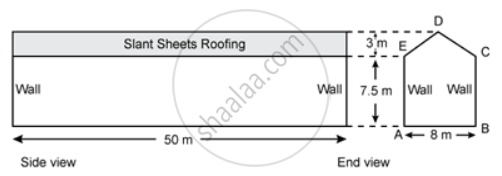
Calculate the total volume content of the shed.
The cross section of a canal is a trapezium with the base length of 3 m and the top length of 5 m. It is 2 m deep and 400 m long. Calculate the volume of water it holds.
