Advertisements
Advertisements
Question
The cross section of a piece of metal 2 m in length
is shown. Calculate the volume of the piece of metal.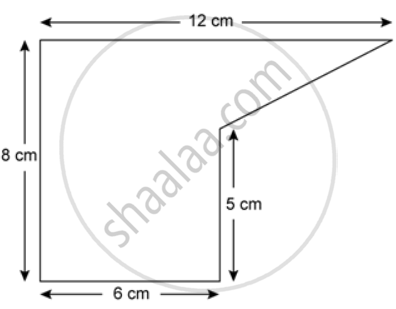
Solution

Length (height) of the metal
= 2m
= 200cm
Volume of the metal
= Area of cross-section x height
= 57 x 200
= 11400cm3
∴ Volume of the metal is 11400cm3.
APPEARS IN
RELATED QUESTIONS
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimeters.
Assume that all angles in the figures are right angles.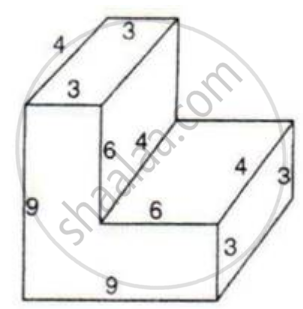
A rectangular cardboard sheet has length 32 cm and breadth 26 cm. Squares each of side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
A rectangular water-tank measuring 80 cm x 60 cm is filled form a pipe of cross-sectional area 1.5 cm2, the water emerging at 3.2 m/s. How long does it take to fill the tank?
The cross section of a piece of metal 2 m in length is shown. Calculate the area of cross section.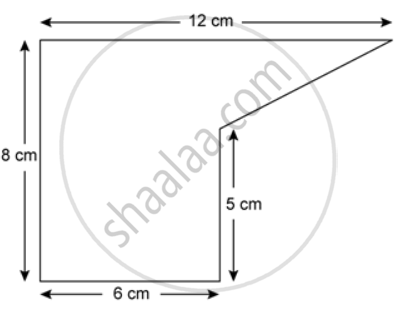
The given figure is a cross -section of a victory stand used in sports. All measurements are in centimetres. Assume all angles in the figure are right angles. If the width of the stand is 60 cm, find The space it occupies in cm3.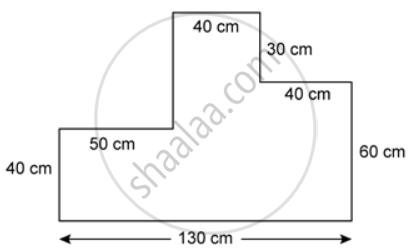
A swimming pool is 50 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 4.5 m respectively. If the bottom of the pool slopes uniformly, find the amount of water in kilolitres required to fill the pool (1 m3 = 1000 liters).
The cross section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the figure. AM = BN; AB = 4.4 m, CD = 3 m The height of a tunnel is 2.4 m. The tunnel is 5.4 m long. Calculate the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per m2.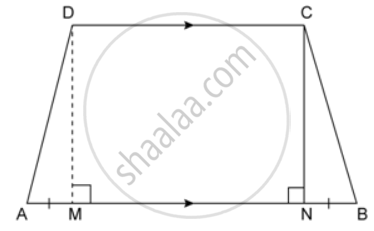
ABCDE is the end view of a factory shed which is 50 m long. The roofing of the shed consists of asbestos sheets as shown in the figure. The two ends of the shed are completely closed by brick walls.
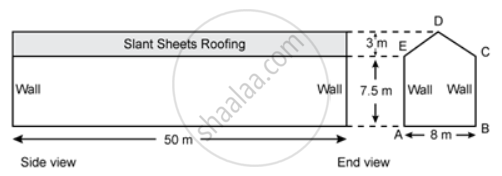
If the cost of asbestos sheet roofing is Rs. 20 per m2, find the cost of roofing.
The cross section of a swimming pool is a trapezium whose shallow and deep ends are 1 m and 3 m respectively. If the length of the pool is 50 m and its width is 1.5 m, calculate the volume of water it holds.
A hose-pipe of cross section area 3 cm2 delivers 1800 liters of water in 10 minutes. Find the speed of water in km/h through the pipe.
