Advertisements
Advertisements
Question
The line through A(–2, 3) and B(4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution
Slope of the line through A(–2, 3) and B(4, b) = `m_1 = (y_2 - y_1)/(x_2 - x_1) = (b - 3)/(4+2) = (b -3)/6`
Equation of given line is 2x - 4y - 5 = 0
`=> 4y = 2x - 5`
`=> y = 1/2 x - 5/4`
∴ Slope of given line = `m_2 = 1/2`
Since the lines are perpendicular therefore `m_1 xx m_2 = -1`
`=> (b - 3)/6 xx 1/2 = -1`
`=> b -3 = -12 => b = -9`
APPEARS IN
RELATED QUESTIONS
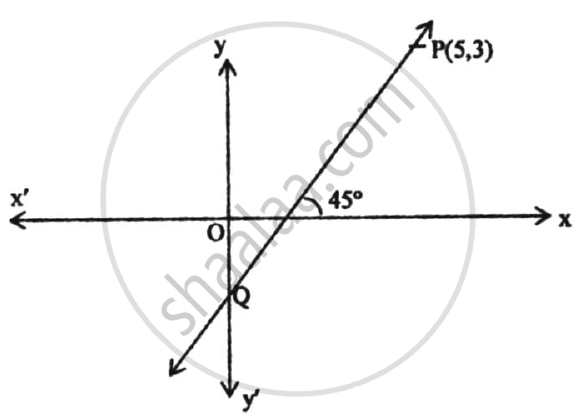
The line through P(5, 3) intersects y-axis at Q.
(1) Write the slope of the line.
(2) Write the equation of the line.
(3) Find the coordinates of Q.
The line passing through (−4, −2) and (2, −3) is perpendicular to the line passing through (a, 5) and (2, −1). Find a.
Without using the distance formula, show that the points A(4, −2), B(−4, 4) and C(10, 6) are the vertices of a right-angled triangle.
A(5, 4), B(−3, −2) and C(1, −8) are the vertices of a triangle ABC. Find:
- the slope of the altitude of AB,
- the slope of the median AD and
- the slope of the line parallel to AC.
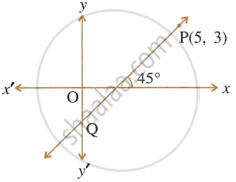
The line through P(5, 3) intersects y-axis at Q.
- Write the slope of the line.
- Write the equation of the line.
- Find the co-ordinates of Q.
Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.
Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel to each other. Find the relation connecting a and b.
Find the slope of the lines passing through the given point.
A(2, 3), B(4, 7)
Find the value, of k, if the line represented by kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other.
If the lines 7y = ax + 4 and 2y = 3 − x, are parallel to each other, then the value of ‘a’ is:
