Advertisements
Advertisements
Question
The marks of 10 students of a class in an examination arranged in ascending order is as follows:
13, 35, 43, 46, x, x + 4, 55, 61, 71, 80
If the median marks is 48, find the value of x. Hence, find the mode of the given data.
Solution
Data in ascending order:
13, 35, 43, 46, x, x + 4, 55, 61, 71, 80
Median = 48
Number of observations = n = 10 ...(Even)
∴ Median = `((n/2)^"th" "term" + (n/2 + 1)^"th" "term")/2`
`=> 48 = ((10/2)^"th" "term" + (10/2 + 1)^"th" "term")/2`
`=> 48 = (5^"th" "term" + 6^"th" "term")/2`
`=> 48 = (x + x + 4)/2`
`=> 48 = (2x + 4)/2`
`=>` 48 = x + 2
`=>` x = 46
`=>` x + 4 = 46 + 4 = 50
Thus, the observations are 13, 35, 43, 46, 46, 50, 55, 61, 71, 80
Since 46 has highest frequency.
Hence, the mode of the data is 46.
APPEARS IN
RELATED QUESTIONS
The ages of 40 students are given in the following table :
| Age (in years) | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Frequency | 2 | 4 | 6 | 9 | 8 | 7 | 4 |
Find the arithmetic mean.
Using the information given in the adjoining histogram, calculate the mean.
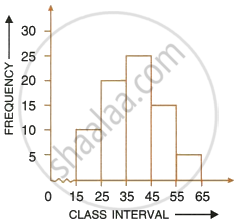
Find the mode of the following data:
9, 11, 8, 11, 16, 9, 11, 5, 3, 11, 17 and 8
The marks of 20 students in a test were as follows:
2, 6, 8, 9, 10, 11, 11, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 18, 19 and 20.
Calculate:
- the mean
- the median
- the mode
Find the mean of the following frequency distribution :
| Class | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
| Frequency | 6 | 10 | 8 | 12 | 4 |
Find the median of the following frequency distribution :
| Salarv fin Rs) | 3500 | 4000 | 4500 | 5000 | 5500 | 6000 |
| No. of people | 9 | 17 | 23 | 15 | 6 | 5 |
Find the median of:
233, 173, 189, 208, 194, 204, 194, 185, 200 and 220.
Find the mean of: all prime numbers between 20 and 40.
3, 8, 10, x, 14, 16, 18, 20 are in the ascending order and their median is 13. Calculate the numerical value of x.
The median of the following observations arranged in ascending order is 64. Find the value of x:
27, 31, 46, 52, x, x + 4, 71, 79, 85, 90
