Advertisements
Advertisements
Question
The ratio of the areas of two triangles with the common base is 4 : 3. Height of the larger triangle is 2 cm, then find the corresponding height of the smaller triangle.
Solution
Let the height of the larger triangle be h1 and that of the smaller triangle be h2.
The ratio of the areas of two triangles with a common base is equal to the ratio of their corresponding heights.
`"Area(larger Triangle)"/"Area(smaller Triangle)"="h"_1/"h"_2`
`4/3=2/"h"_2`
`4xx "h"_2=3xx2`
`therefore"h"_2=(3xx2)/4=6/4`
`therefore"h"_2=1.5" cm"`
The corresponding height of the smaller triangle is 1.5 cm.
APPEARS IN
RELATED QUESTIONS
In the following figure RP: PK= 3:2, then find the value of A(ΔTRP):A(ΔTPK).

The ratio of the areas of two triangles with common base is 6:5. Height of the larger triangle of 9 cm, then find the corresponding height of the smaller triangle.
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
In adjoining figure, PQ ⊥ BC, AD ⊥ BC then find following ratios.
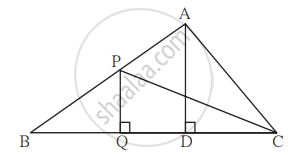
- `("A"(∆"PQB"))/("A"(∆"PBC"))`
- `("A"(∆"PBC"))/("A"(∆"ABC"))`
- `("A"(∆"ABC"))/("A"(∆"ADC"))`
- `("A"(∆"ADC"))/("A"(∆"PQC"))`
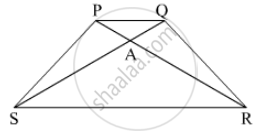
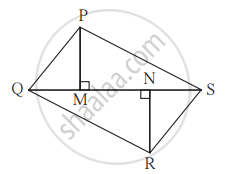
In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
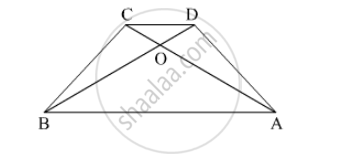
In trapezium ABCD, side AB || side DC, diagonals AC and BD intersect in point O. If AB = 20, DC = 6, OB = 15 then Find OD.
In ∆ABC, B - D - C and BD = 7, BC = 20 then find following ratio.
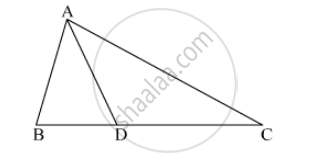
`"A(∆ ABD)"/"A(∆ ADC)"`
In the figure, PM = 10 cm, A(∆PQS) = 100 sq.cm, A(∆QRS) = 110 sq. cm, then find NR.
In ∆ABC, B – D – C and BD = 7, BC = 20, then find the following ratio.
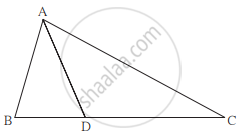
`(A(∆ABD))/(A(∆ABC))`
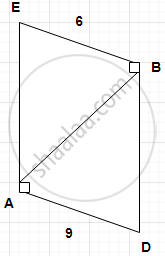
In the given, seg BE ⊥ seg AB and seg BA ⊥ seg AD.
if BE = 6 and AD = 9 find `(A(Δ ABE))/(A(Δ BAD))`.
A roller of diameter 0.9 m and the length 1.8 m is used to press the ground. Find the area of the ground pressed by it in 500 revolutions.
`(pi=3.14)`
If ΔXYZ ~ ΔPQR then `"XY"/"PQ" = "YZ"/"QR"` = ?
Ratio of corresponding sides of two similar triangles is 4:7, then find the ratio of their areas = ?
In fig. BD = 8, BC = 12, B-D-C, then `"A(ΔABC)"/"A(ΔABD)"` = ?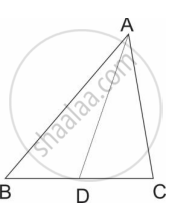
Prove that, The areas of two triangles with the same height are in proportion to their corresponding bases. To prove this theorem start as follows:
- Draw two triangles, give the names of all points, and show heights.
- Write 'Given' and 'To prove' from the figure drawn.
If ΔABC ∼ ΔDEF, length of side AB is 9 cm and length of side DE is 12 cm, then find the ratio of their corresponding areas.
In the figure, PQ ⊥ BC, AD ⊥ BC. To find the ratio of A(ΔPQB) and A(ΔPBC), complete the following activity.
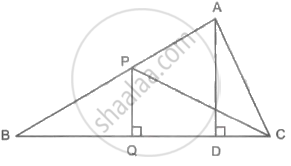
Given: PQ ⊥ BC, AD ⊥ BC
Now, A(ΔPQB) = `1/2 xx square xx square`
A(ΔPBC) = `1/2 xx square xx square`
Therefore,
`(A(ΔPQB))/(A(ΔPBC)) = (1/2 xx square xx square)/(1/2 xx square xx square)`
= `square/square`
