Advertisements
Advertisements
Question
Using vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
Solution
Let ABCD and ABFE be two parallelograms on the same base AB and between same parallel lines AB and DF.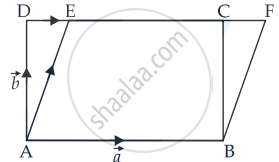
Let `vec"AB" = vec"a"` and `vec"AD" = vec"b"`
∴ Area of parallelogram ABCD = `|vec"a" xx vec"b"|`
= `|vec"a" xx (vec"AD" + vec"DE")|`
= `|vec"a" xx (vec"b" xx "K"vec"a")|`
= `|(vec"a" xx vec"b") + "K"(vec"a" xx vec"a")`
= `|vec"a" xx vec"b"| + 0` ...`["becuase" vec"a" xx vec"a" = 0]`
= `|vec"a" xx vec"b"|`
Hence proved.
APPEARS IN
RELATED QUESTIONS
If a unit vector `veca` makes angles `pi/3` with `hati,pi/4` with `hatj` and acute angles θ with ` hatk,` then find the value of θ.
If `veca=hati+2hatj-hatk, vecb=2hati+hatj+hatk and vecc=5hati-4hatj+3hatk` then find the value of `(veca+vecb).vec c`
If `veca=2hati+hatj+3hatk and vecb=3hati+5hatj-2hatk` ,then find ` |veca xx vecb|`
Find x such that the four points A(4, 1, 2), B(5, x, 6) , C(5, 1, -1) and D(7, 4, 0) are coplanar.
A line passing through the point A with position vector `veca=4hati+2hatj+2hatk` is parallel to the vector `vecb=2hati+3hatj+6hatk` . Find the length of the perpendicular drawn on this line from a point P with vector `vecr_1=hati+2hatj+3hatk`
if `|vecaxxvecb|^2+|veca.vecb|^2=400 ` and `|vec a| = 5` , then write the value of `|vecb|`
If `vecr=xhati+yhatj+zhatk` ,find `(vecrxxhati).(vecrxxhatj)+xy`
Find `veca.(vecbxxvecc), " if " veca=2hati+hatj+3hatk, vecb=-hati+2hatj+hatk " and " vecc=3hati+hatj+2hatk`
Find the angle between the vectors `2hat"i" - hat"j" + hat"k"` and `3hat"i" + 4hat"j" - hat"k"`.
If `vec"a" + vec"b" + vec"c"` = 0, show that `vec"a" xx vec"b" = vec"b" xx vec"c" = vec"c" xx vec"a"`. Interpret the result geometrically?
Using vectors, find the area of the triangle ABC with vertices A(1, 2, 3), B(2, – 1, 4) and C(4, 5, – 1).
Show that area of the parallelogram whose diagonals are given by `vec"a"` and `vec"b"` is `(|vec"a" xx vec"b"|)/2`. Also find the area of the parallelogram whose diagonals are `2hat"i" - hat"j" + hat"k"` and `hat"i" + 3hat"j" - hat"k"`.
If `vec"a" = hat"i" + hat"j" + hat"k"` and `vec"b" = hat"j" - hat"k"`, find a vector `vec"c"` such that `vec"a" xx vec"c" = vec"b"` and `vec"a"*vec"c"` = 3.
The value of λ for which the vectors `3hat"i" - 6hat"j" + hat"k"` and `2hat"i" - 4hat"j" + lambdahat"k"` are parallel is ______.
The vectors from origin to the points A and B are `vec"a" = 2hat"i" - 3hat"j" + 2hat"k"` and `vec"b" = 2hat"i" + 3hat"j" + hat"k"`, respectively, then the area of triangle OAB is ______.
If `|vec"a"|` = 10, `|vec"b"|` = 2 and `vec"a".vec"b"` = 12, then value of `|vec"a" xx vec"b"|` is ______.
The vectors `lambdahat"i" + hat"j" + 2hat"k", hat"i" + lambdahat"j" - hat"k"` and `2hat"i" - hat"j" + lambdahat"k"` are coplanar if ______.
If `|vec"a"|` = 4 and −3 ≤ λ ≤ 2, then the range of `|lambdavec"a"|` is ______.
The value of the expression `|vec"a" xx vec"b"|^2 + (vec"a".vec"b")^2` is ______.
If `|vec"a" xx vec"b"|^2 + |vec"a".vec"b"|^2` = 144 and `|vec"a"|` = 4, then `|vec"b"|` is equal to ______.
