SSC (English Medium)
SSC (Marathi Semi-English)
Academic Year: 2018-2019
Date: July 2019
Advertisements
Point M is the mid-point of segment AB. If AB = 8.6 cm, then find AM.
Chapter: [0.05] Co-ordinate Geometry
Write the equations of the x-axis and y-axis.
Chapter: [0.05] Co-ordinate Geometry

In the above figure, line l || line m and line n is a transversal. Using the given information find the value of x.
Chapter: [0.01] Similarity
If sin θ = `1/2`, then find the value of θ.
Chapter: [0.06] Trigonometry
If the side of a cube is 5 cm, then find its volume.
Chapter: [0.07] Mensuration
In ΔDEF, if ∠E = 90°, then find the value of ∠D + ∠F.
Chapter: [0.02] Pythagoras Theorem
Draw seg AB = 6.8 cm and draw perpendicular bisector of it.
Chapter: [0.01] Similarity
If ΔABC ~ ΔDEF, then writes the corresponding congruent angles and also write the ratio of corresponding sides.
Chapter: [0.01] Similarity
The perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
Chapter: [0.03] Circle
Advertisements
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
30°
60°
90°
45°
Chapter: [0.02] Pythagoras Theorem
Choose the correct alternative:
If ΔABC ~ ΔPQR and 4A (ΔABC) = 25 A(ΔPQR), then AB : PQ = ?
4:25
2:5
5:2
25:4
Chapter: [0.01] Similarity
Choose the correct alternative:
If the points, A, B, C are non-collinear points, then how many circles can be drawn which passes through points A, B, and C?
two
three
one
infinite
Chapter: [0.03] Circle
Choose the correct alternative:
sinθ × cosecθ =?
`sqrt(2)`
`1/2`
0
1
Chapter: [0.06] Trigonometry
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Chapter: [0.03] Circle
Find the slope of the line passing through the points A(4,7) and B(2,3).
Chapter: [0.05] Co-ordinate Geometry
If the length of an arc of the sector of a circle is 20 cm and if the radius is 7 cm, find the area of the sector.
Chapter: [0.03] Circle

In the above figure, line AB || line CD || line EF, line l, and line m are its transversals. If AC = 6, CE = 9. BD = 8, then complete the following activity to find DF.
Activity :
`"AC"/"" = ""/"DF"` (Property of three parallel lines and their transversal)
∴ `6/9 = ""/"DF"`
∴ `"DF" = "___"`
Chapter: [0.01] Similarity
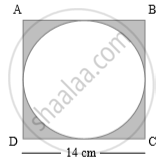
A circle is inscribed in square ABCD of side 14 cm. Complete the following activity to find the area of the shaded portion.
Activity:
Area of square ABCD = ______
= 142
= 196 cm2
Area of circle = πr2 = `22/7xx 7^2`
= ____ cm2
Area of shaded portion = Area of square ABCD – Area of circle
= 196 – _______
= _____ cm2
Chapter: [0.07] Mensuration
In the following figure, O is the centre of the circle. ∠ABC is inscribed in arc ABC and ∠ ABC = 65°. Complete the following activity to find the measure of ∠AOC.
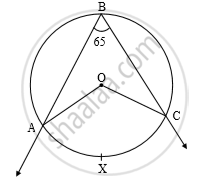
∠ABC = `1/2`m ______ (Inscribed angle theorem)
______ × 2 = m(arc AXC)
m(arc AXC) = _______
∠AOC = m(arc AXC) (Definition of measure of an arc)
∠AOC = ______
Chapter: [0.03] Circle
Advertisements
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
Chapter: [0.02] Pythagoras Theorem
Find the co-ordinates of the centroid of the Δ PQR, whose vertices are P(3, –5), Q(4, 3) and R(11, –4)
Chapter: [0.04] Geometric Constructions [0.05] Co-ordinate Geometry
If cosθ = `5/13`, then find sinθ.
Chapter: [0.06] Trigonometry
Verify that the points A(–2, 2), B(2, 2) and C(2, 7) are the vertices of a right-angled triangle.
Chapter: [0.06] Trigonometry
Prove that:
Chapter: [0.06] Trigonometry
In ΔABC, seg AP is a median. If BC = 18, AB2 + AC2 = 260, then find the length of AP.
Chapter: [0.02] Pythagoras Theorem
∆ABC ~ ∆LMN. In ∆ABC, AB = 5.5 cm, BC = 6 cm, CA = 4.5 cm. Construct ∆ABC and ∆LMN such that `"BC"/"MN" = 5/4`.
Chapter: [0.04] Geometric Constructions

In the above figure, seg PA, seg QB and RC are perpendicular to seg AC. From the information given in the figure, prove that: `1/x + 1/y = 1/z`
Chapter: [0.05] Co-ordinate Geometry
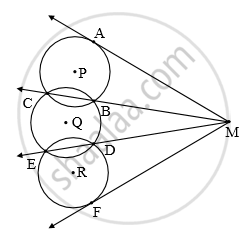
In the above figure, the circles with P, Q, and R intersect at points B, C, D, and E as shown. Lines CB and ED intersect in point M. Lines are drawn from point M to touch the circles at points A and F. Prove that MA = MF.
Chapter: [0.03] Circle

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Chapter: [0.03] Circle

In the above figure, a sphere is placed in a cylinder. It touches the top, bottom and curved surface of the cylinder. If the radius of the base of the cylinder is ‘r’, write the answer to the following questions.
a. What is the height of the cylinder in terms of ‘r’?
b. What is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
c. What is the ratio of volumes of the cylinder and of the sphere?
Chapter: [0.07] Mensuration
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 10th Standard Board Exam Geometry Mathematics 2 with solutions 2018 - 2019
Previous year Question paper for Maharashtra State Board 10th Standard Board Exam Geometry Maths 2-2019 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Geometry Mathematics 2, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 10th Standard Board Exam.
How Maharashtra State Board 10th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Geometry Mathematics 2 will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
