BE Civil Engineering
BE Computer Engineering
BE Mechanical Engineering
BE Biotechnology
BE Marine Engineering
BE Printing and Packaging Technology
BE Production Engineering
BE IT (Information Technology)
BE Electrical Engineering
BE Electronics and Telecommunication Engineering
BE Instrumentation Engineering
BE Electronics Engineering
BE Chemical Engineering
BE Construction Engineering
BE Biomedical Engineering
BE Automobile Engineering
Academic Year: 2016-2017
Date: December 2016
Advertisements
(1) Question no. 1 is compulsory.
(2) Attempt any 3 questions from remaining five questions.
If `cos alpha cos beta=x/2, sinalpha sinbeta=y/2`, prove that:
`sec(alpha -ibeta)+sec(alpha-ibeta)=(4x)/(x^2-y^2)`
Chapter: [5] Complex Numbers
If `z =log(e^x+e^y) "show that rt" - s^2 = 0 "where r"= (del^2z)/(delx^2),t=(del^2z)/(dely^2)"s"=(del^2z)/(delx dely)`
Chapter: [5] Complex Numbers
If x = uv, y `=(u+v)/(u-v).`find `(del(u,v))/(del(x,y))`.
Chapter: [5] Complex Numbers
If `y=2^xsin^2x cosx` find `y_n`
Chapter: [5] Complex Numbers
Express the matrix as the sum of symmetric and skew symmetric matrices.
Chapter: [7] Matrices
Evaluat `lim_(x->0) (e^(2x)-(1+x)^2)/(xlog(1+x)`
Chapter: [10] Indeterminate Forms, Numerical Solutions of Transcendental Equations and System of Linear Equations
Show that the roots of x5 =1 can be written as 1, `alpha^1,alpha^2,alpha^3,alpha^4` .hence show that `(1-alpha^1) (1-alpha^2) (1-alpha^3)(1-alpha^4)=5.`
Chapter: [5] Complex Numbers
Advertisements
Reduce the following matrix to its normal form and hence find its rank.
Chapter: [7] Matrices
Solve the following equation by Gauss-Seidel method upto four iterations
4x-2y-z=40, x-6y+2y=-28, x-2y+12z=-86.
Chapter: [10] Indeterminate Forms, Numerical Solutions of Transcendental Equations and System of Linear Equations
Investigate for what values of μ and λ the equations x+y+z=6, x+2y+3z=10, x+2y+λz=μ has
1) No solution
2) A unique solution
3) Infinite number of solutions.
Chapter: [7] Matrices
If `u=x^2+y^2+z^2` where `x=e^t, y=e^tsint,z=e^tcost`
Prove that `(du)/(dt)=4e^(2t)`
Chapter: [5] Complex Numbers
Show that `sin(e^x-1)=x^1+x^2/2-(5x^4)/24+`...................
Chapter: [9] Applications of Partial Differentiation , Expansion of Functions
Expand `2x^3+7x^2+x-6` in powers of (x-2)
Chapter: [5] Complex Numbers
If x = u+v+w, y = uv+vw+uw, z = uvw and φ is a function of x, y and z
Prove that 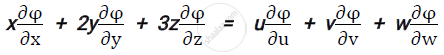
Chapter: [8] Partial Differentiation
Advertisements
If tan(θ+iφ)=tanα+isecα
Prove that
1)`e^(2varphi)=cot(varphi/2)`
2) `2theta=npi+pi/2+alpha`
Chapter: [8] Partial Differentiation
Find the roots of the equation `x^4+x^3 -7x^2-x+5 = 0` which lies between 2 and 2.1 correct to 3 places of decimals using Regula Falsi method.
Chapter: [10] Indeterminate Forms, Numerical Solutions of Transcendental Equations and System of Linear Equations
If y=(x+√x2-1 ,Prove that
`(x^2-1)y_(n+2)+(2n+1)xy_(n+1)+(n^2-m^2)y_n=0`
Chapter: [6.01] Successive Differentiation
Using the encoding matrix `[(1,1),(0,1)]` encode and decode the messag I*LOVE*MUMBAI.
Chapter: [7] Matrices
Considering only principal values separate into real and imaginary parts
`i^((log)(i+1))`
Chapter: [6.02] Logarithm of Complex Numbers
Show that `ilog((x-i)/(x+i))=pi-2tan6-1x`
Chapter: [6.02] Logarithm of Complex Numbers
Using De Moivre’s theorem prove that]
`cos^6theta-sin^6theta=1/16(cos6theta+15cos2theta)`
Chapter: [5] Complex Numbers
If u `=sin^(-1)((x^(1/3)+y^(1/3))/(x^(1/2)-y^(1/2)))`, Prove that
`x^2(del^2u)/(delx^2)+2xy(del^2u)/(delxdely)+y^2(del^2u)/(dely^2)=tanu/144(tan^2u+13)`
Chapter: [7] Matrices
Find the maxima and minima of `x^3 y^2(1-x-y)`
Chapter: [9] Applications of Partial Differentiation , Expansion of Functions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
University of Mumbai previous year question papers Semester 1 (FE First Year) Applied Mathematics 1 with solutions 2016 - 2017
Previous year Question paper for University of Mumbai Semester 1 (FE First Year) Applied Mathematics 1-2017 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Applied Mathematics 1, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of University of Mumbai Semester 1 (FE First Year).
How University of Mumbai Semester 1 (FE First Year) Question Paper solutions Help Students ?
• Question paper solutions for Applied Mathematics 1 will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
