Advertisements
Advertisements
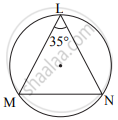
ऊपर दी गई आकृति में, ∠L = 35° तो
- m(चाप MN)
- m(चाप MLN)
ज्ञात कीजिए।
हल:
- ∠L = `1/2` m(चाप MN) ............(अंतर्लिखित कोण का प्रमेय)
∴ `square = 1/2` m(चाप MN)
∴ 2 × 35 = m(चाप MN)
∴ m(चाप MN) = `square` - m(चाप MLN) = `square` - m(चाप MN) ...........(चापों के मापों का योग गुणधर्म)
= 360° - 70°
∴ m(चाप MLN) = `square`
Concept: अंतर्लिखित कोण का प्रमेय
सिद्ध कीजिए कि, “एक की चाप में अंतर्लिखित कोण सर्वांगसम होते हैं।”
Concept: अंतर्लिखित कोण के प्रमेय का उपप्रमेय
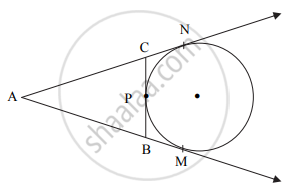
ΔABC में, भुजा BC को एक वृत्त बाह्यभाग में स्पर्श करता है। उसी प्रकार भुजा AC और भुजा AB को आगे बढ़ाने पर यह वृत्त को बिन्दु N तथा बिन्दु M पर स्पर्श करता है, तो सिद्ध कीजिए: AM = `1/2`(ΔABC की परिमिति)
Concept: स्पर्शरेखाखंड का प्रमेय (Tangent Segment Theorem)
3 सेमी त्रिज्या वाले वृत्त की सबसे बड़ी जीवा लंबाई = ?
Concept: जीवाओं का अंतःछेदन प्रमेय (Theorem of Internal Division of Chords)
5 सेमी तथा 3 सेमी त्रिज्या वाले दो वृत्त परस्पर बाह्यस्पर्श करते हैं, तो उनके केंद्रों के बीच की दूरी ज्ञात कीजिए।
Concept: स्पर्श वृत्त प्रमेय (Theorem of Touching Circles)

ऊपर दी गयी आकृति में, ∠ABC यह चाप ABC में अंतर्लिखित कोण है।
यदि ∠ABC = 60%, तो m ∠AOC ज्ञात कीजिए।
हल:
∠ABC = `1/2`m (चाप AXC) ...... `square`
60° = `1/2` m (चाप AXC)
`square` = m (चाप AXC)
परंतु m ∠ AOC = m(चाप`square`) ......(केंद्रीय कोण का गुणधर्म)
∴ m ∠AOC = `square`
Concept: अंतर्लिखित कोण का प्रमेय
'O' केंद्र तथा 3 सेमी त्रिज्या का एक वृत्त बनाइए।वृत्त के बाहर स्थित बिंदु P से स्पर्श रेखाखंड PA तथा PB इस प्रकार बनाइये कि ∠APB = 70°
Concept: स्पर्श रेखा - त्रिज्या प्रमेय का विलोम
‘O’ केंद्र वाले वृत्त की रेख AB जीवा है। AOC वृत्त का व्यास है। AT वृत्त के बिंदु A पर बनी स्पर्शरेखा है।
इस आधार पर नीचे दिए प्रश्नों के उत्तर लिखिए:
- दी गई जानकारी के आधार पर आकृति बनाइये।
- ∠CAT तथा ∠ABC की माप ज्ञात करने के लिए संबंधित प्रमेय का कथन लिखिए।
- क्या ∠CAT तथा ∠ABC एकरूप हैं? अपने उत्तर की पुष्टि कीजिये।
Concept: वृत्त
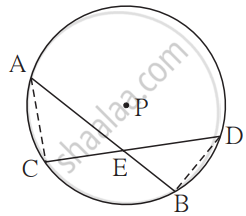
दत्त: वृत्त का केंद्र P है। जीवा AB और जीवा CD परस्पर बिंदु E पर प्रतिच्छेदित करती हैं।
साध्य: AE × EB = CE × ED
रचना: रेख AC और रेख DB खींचिए।
खाली जगह भरकर उपपत्ति पूर्ण कीजिए।
उपपत्ति: ΔCAE और ΔBDE में,
∠AEC ≅ ∠DEB ......... `square`
`square` ≅ ∠BDE .....(एक ही चाप में अंतर्लिखित कोण)
∴ ΔCAE ~ ΔBDE ........ `square`
∴ `square/ ("DE") = ("CE")/square` ........ `square`
∴ AE × EB = CE × ED
Concept: जीवाओं का अंतःछेदन प्रमेय (Theorem of Internal Division of Chords)
ΔABC ~ ΔLMN , ΔABC में AB = 5.5 सेमी, BC = 6 सेमी, CA = 4.5 सेमी और `"BC"/"MN"` = `5/4` तो ΔABC तथा ΔLMN की रचना कीजिए।
Concept: समरूप त्रिभुजों की रचना
3.3 सेमी त्रिज्यावाला एक वृत्त बनाइए। वृत्त में 6.6 सेमी लंबाई वाली एक जीवा PQ खींचिए। स्पर्श रेखा के संदर्भ में अपने निरीक्षण दर्ज कीजिए।
Concept: वृत्त के बाह्य भाग में स्थित किसी बिंदु से वृत्त पर स्पर्शरेखा खींचना
4.1 सेमी त्रिज्यावाला एक वृत्त खींचिए। वृत्त के केंद्र से 7.3 सेमी दूर स्थित बिंदु से स्पर्श रेखा खींचिए।
Concept: वृत्त के बाह्य भाग में स्थित किसी बिंदु से वृत्त पर स्पर्शरेखा खींचना
बिंदु ‘O’ केंद्र तथा त्रिज्या 3.2 सेमी लेकर एक वृत्त खींचो। वृत्त पर कोई बिंदु P लेकर, वृत्त-केंद्र का उपयोग करते हुए बिंदु P से वृत्त की स्पर्श रेखा खींचो।
Concept: वृत्त पर स्थित किसी बिंदु से वृत्त की स्पर्शरेखा खींचन : वृत्त केंद्र का उपयोग करते हुए
ΔABC ∼ ΔPQR, ΔABC में AB = 5.4 सेमी, BC = 4.2 सेमी, AC = 6 सेमी, AB:PQ = 3:2 है, तो ΔABC तथा ΔPQR की रचना करो।
Concept: समरूप त्रिभुजों की रचना
ΔSHR ∼ ΔSVU, ΔSHR में SH = 4.5 सेमी, HR = 5.2 सेमी, SR = 5.8 सेमी तथा `"SH"/"SV" = 3/5` तो ΔSVU की रचना कीजिए।
Concept: समरूप त्रिभुजों की रचना
किसी रेखा द्वारा X-अक्ष की धन दिशा की ओर निर्मित कोण का माप दिया गया है, इस आधार पर रेखा का ढाल ज्ञात कीजिए।
45°
Concept: रेखा का ढाल (Slope of a Line)
नीचे दिए गए बिंदुओं से होकर जानेवाली रेखा का ढाल ज्ञात कीजिए।
A (2, 3) और B (4, 7)
Concept: रेखा का ढाल (Slope of a Line)
निम्नलिखित बिंदु एक रेखीय हैं या नहीं? जाँच कीजिए।
A(-1, -1), B(0, 1), C(1, 3)
Concept: रेखा का ढाल (Slope of a Line)
सिद्ध कीजिए कि, बिंदु P(1, −2), Q(5, 2), R(3, −1) और S(−1, −5) समांतर चतुर्भुज के शीर्षबिंदु हैं।
Concept: दूरी सूत्र
यदि D(-7, 6), E(8, 5) और F(2, -2) त्रिभुज की भुजाओं के मध्य बिंदु हों तो उस त्रिभुज के केंद्रक बिंदु के निर्देशांक ज्ञात कीजिए।
Concept: केंद्रव बिंदु का सूत्र (माध्यिका संगामी बिंदु का सूत्र) (Centroid Formula)
