Advertisements
Advertisements
प्रश्न
A bag contains 5 red, 6 white and 7 black balls. Two balls are drawn at random. What is the probability that both balls are red or both are black?
उत्तर
There are 18 balls in the bag out of which two balls can be drawn in 18C2 ways.
So, total number of elementary events = 18C2 = 153
According to the question, both the balls drwan are either red or black, which means that the two balls should be of the same colour.
Out of five red balls, two red balls can be drawn in 5C2 ways.
Similarly, two black balls can be drawn from seven black balls in 7C2 ways.
So, favourable number of elementary events = 5C2 + 7C2 = 10 + 21 = 31
Hence, required probability = \[\frac{31}{153}\]
APPEARS IN
संबंधित प्रश्न
A coin is tossed twice, what is the probability that at least one tail occurs?
A card is selected from a pack of 52 cards.
- How many points are there in the sample space?
- Calculate the probability that the card is an ace of spades.
- Calculate the probability that the card is
- an ace
- black card.
A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. Find the probability that the sum of numbers that turn up is (i) 3 (ii) 12
There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?
Check whether the following probabilities P(A) and P(B) are consistently defined
P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8
Fill in the blank in following table:
| P(A) | P(B) | P(A ∩ B) | P(A ∪ B) |
| 0.35 | ... | 0.25 | 0.6 |
A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that all will be blue?
From the employees of a company, 5 persons are selected to represent them in the managing committee of the company. Particulars of five persons are as follows:
| S. No. | Name | Sex | Age in years |
| 1. | Harish | M | 30 |
| 2. | Rohan | M | 33 |
| 3. | Sheetal | F | 46 |
| 4. | Alis | F | 28 |
| 5. | Salim | M | 41 |
A person is selected at random from this group to act as a spokesperson. What is the probability that the spokesperson will be either male or over 35 years?
The number lock of a suitcase has 4 wheels, each labelled with ten digits i.e., from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the right sequence to open the suitcase?
A and B throw a pair of dice. If A throws 9, find B's chance of throwing a higher number.
Two unbiased dice are thrown. Find the probability that the sum of the numbers obtained on the two dice is neither a multiple of 2 nor a multiple of 3
A bag contains 8 red, 3 white and 9 blue balls. If three balls are drawn at random, determine the probability that all the balls are of different colours.
If a letter is chosen at random from the English alphabet, find the probability that the letter is a vowel .
If a letter is chosen at random from the English alphabet, find the probability that the letter is a consonant .
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (ii) |
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
\[\frac{1}{7}\]
|
Which of the cannot be valid assignment of probability for elementary events or outcomes of sample space S = {w1, w2, w3, w4, w5, w6, w7}:
| Elementary events: | w1 | w2 | w3 | w4 | w5 | w6 | w7 |
| (iv) |
\[\frac{1}{14}\]
|
\[\frac{2}{14}\]
|
\[\frac{3}{14}\]
|
\[\frac{4}{14}\]
|
\[\frac{5}{14}\]
|
\[\frac{6}{14}\]
|
\[\frac{15}{14}\]
|
In a single throw of three dice, find the probability of getting the same number on all the three dice.
A box contains 100 bulbs, 20 of which are defective. 10 bulbs are selected for inspection. Find the probability that: all 10 are defective
In a leap year the probability of having 53 Sundays or 53 Mondays is ______.
Three-digit numbers are formed using the digits 0, 2, 4, 6, 8. A number is chosen at random out of these numbers. What is the probability that this number has the same digits?
If the letters of the word ALGORITHM are arranged at random in a row what is the probability the letters GOR must remain together as a unit?
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine P(A)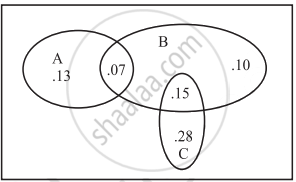
The accompanying Venn diagram shows three events, A, B, and C, and also the probabilities of the various intersections (for instance, P(A ∩ B) = .07). Determine `P(A ∩ barB)`
If the letters of the word ASSASSINATION are arranged at random. Find the probability that two I’s and two N’s come together
If the letters of the word ASSASSINATION are arranged at random. Find the probability that no two A’s are coming together
Seven persons are to be seated in a row. The probability that two particular persons sit next to each other is ______.
Without repetition of the numbers, four-digit numbers are formed with the numbers 0, 2, 3, 5. The probability of such a number divisible by 5 is ______.
6 boys and 6 girls sit in a row at random. The probability that all the girls sit together is ______.
A single letter is selected at random from the word ‘PROBABILITY’. The probability that it is a vowel is ______.
If the probabilities for A to fail in an examination is 0.2 and that for B is 0.3, then the probability that either A or B fails is ______.
The probability that a student will pass his examination is 0.73, the probability of the student getting a compartment is 0.13, and the probability that the student will either pass or get compartment is 0.96.
The probabilities that a typist will make 0, 1, 2, 3, 4, 5 or more mistakes in typing a report are, respectively, 0.12, 0.25, 0.36, 0.14, 0.08, 0.11.
If A and B are two candidates seeking admission in an engineering College. The probability that A is selected is .5 and the probability that both A and B are selected is at most .3. Is it possible that the probability of B getting selected is 0.7?
The probability that the home team will win an upcoming football game is 0.77, the probability that it will tie the game is 0.08, and the probability that it will lose the game is ______.
A box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?
If 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when, the repetition of digits is not allowed?
