Question

A carrom board (4 ft × 4 ft square) has the queen at the centre. The queen, hit by the striker moves to the from edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen (a) from the centre to the front edge, (b) from the front edge to the hole and (c) from the centre to the hole.

Answer 1

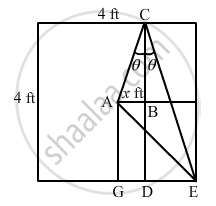
Consider that the queen is initially at point A as shown in the figure.
Let AB be x ft.
So, DE = (2  \[-\] x) ft
In ∆ABC, we have: \[\tan \theta = \frac{x}{2}\] ...(i)
Also, in ∆DCE, we have:

\[\tan \theta = \frac{\left( 2 - x \right)}{4}\] ...(ii)
From (i) and (ii), we get: 

\[\frac{x}{2} = \frac{\left( 2 - x \right)}{4}\]

\[ \Rightarrow 2\left( 2 - x \right) = 4x\]

\[ \Rightarrow 4 - 2x = 4x\]

\[ \Rightarrow 6x = 4\]

\[ \Rightarrow x = \frac{2}{3}\text { ft }\]

(a) In ∆ABC, we have:

\[AC = \sqrt{{AB}^2 + {BC}^2}\]

\[= \sqrt{\left( \frac{2}{3} \right)^2 + 2^2}\]

\[ = \sqrt{\frac{4}{9} + 4} = \sqrt{\frac{40}{9}}\]

\[ = \frac{2}{3}\sqrt{10} \text { ft }\]

(b) In ∆CDE, we have:
DE \[= 2 - \frac{2}{3} = \frac{6 - 2}{3} = \frac{4}{3} \text { ft }\]

CD = 4 ft 

\[\therefore CE = \sqrt{{CD}^2 + {DE}^2}\]

\[ = \sqrt{4^2 + \left( \frac{4}{3} \right)^2}\]

\[ = \frac{4}{3}\sqrt{10} \text { ft }\]

(c) In ∆AGE, we have:

\[AE = \sqrt{{AG}^2 + {GE}^2}\]

\[= \sqrt{2^2 + 2^2}\]

\[\sqrt{8} = 2\sqrt{2}\text { ft }\]