Advertisements
Advertisements
प्रश्न
A concave mirror forms an image of 20 cm high object on a screen placed 5.0 m away from the mirror. The height of the image is 50 cm. Find the focal length of the mirror and the distance between the mirror and the object.
उत्तर
Given,
Height of the object, h1 = 20 cm,
Distance of image from screen v = −5.0 m = −500 cm,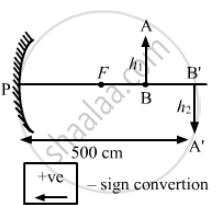
\[- \frac{v}{u} = \frac{h_2}{h_1}\]
\[or \frac{- ( - 500)}{u} = \frac{50}{20}\]
Where 'u' is the distance of object from screen.
(As the image is inverted)
Using mirror formula,
\[\frac{1}{v} + \frac{1}{u} = \frac{1}{f}\]
\[or \frac{1}{- 5} + \frac{1}{- 2} = \frac{1}{f}\]
\[or - \frac{1}{f} = \frac{7}{10}\]
\[or f = - \frac{10}{7} = - 1 . 44 \text{ m }\]
Hence, the required focal length of the concave mirror is 1.44 m.
APPEARS IN
संबंधित प्रश्न
Name the phenomenon responsible for it.
Write two points of difference between the phenomena of interference and diffraction.
In the meterbridge experimental set up, shown in the figure, the null point ‘D’ is obtained at a distance of 40 cm from end A of the meterbridge wire. If a resistance of 10Ω is connected in series with R1, null point is obtained at AD = 60 cm. Calculate the values of R1 and R2.
Describe briefly using a diagram how sunlight is polarised ?
A concave mirror has a focal length of 20 cm. Find the position or positions of an object for which the image-size is double of the object-size.
A candle flame 1.6 cm high is imaged in a ball bearing of diameter 0.4 cm. If the ball bearing is 20 cm away from the flame, find the location and the height of the image.
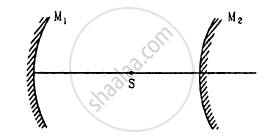
A converging mirror M1, a point source S and a diverging mirror M2 are arranged as shown in figure. The source is placed at a distance of 30 cm from M1. The focal length of each of the mirrors is 20 cm. Consider only the images formed by a maximum of two reflections. It is found that one image is formed on the source itself. (a) Find the distance between the two mirrors. (b) Find the location of the image formed by the single reflection from M2.
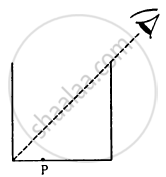
Locate the image of the point P as seen by the eye in the figure.

A cylindrical vessel, whose diameter and height both are equal to 30 cm, is placed on a horizontal surface and a small particle P is placed in it at a distance of 5.0 cm from the centre. An eye is placed at a position such that the edge of the bottom is just visible (see figure). The particle P is in the plane of drawing. Up to what minimum height should water be poured in the vessel to make the particle P visible?
One end of a cylindrical glass rod (μ = 1.5) of radius 1.0 cm is rounded in the shape of a hemisphere. The rod is immersed in water (μ = 4/3) and an object is placed in the water along the axis of the rod at a distance of 8.0 cm from the rounded edge. Locate the image of the object.
The diameter of the sun is 1.4 × 109 m and its distance from the earth is 1.5 × 1011 m. Find the radius of the image of the sun formed by a lens of focal length 20 cm.
Explain: ‘How is a rainbow formed’?
Answer the following question in detail.
Explain the formation of a secondary rainbow. For which angular range with the horizontal is it visible?
Answer the following question in detail.
Is it possible to see primary and secondary rainbow simultaneously? Under what conditions?
Rainbow is the phenomenon due to ______.
Explain the formation of primary and secondary rainbow.
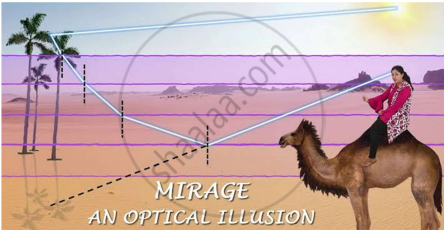
| Case study: Mirage in deserts |
 |
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question : |
A diver at a depth 12 m inside water `(a_(µω) = 4/3)` sees the sky in a cone of semi-vertical angle
