Advertisements
Advertisements
प्रश्न
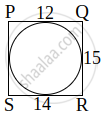
A quadrilateral PQRS is drawn to circumscribe a circle. If PQ = 12 cm, QR = 15 cm and RS = 14 cm, then find the length of SP is ______.
विकल्प
15 cm
14 cm
12 cm
11 cm
उत्तर
A quadrilateral PQRS is drawn to circumscribe a circle. If PQ = 12 cm, QR = 15 cm and RS = 14 cm, then find the length of SP is 11 cm.
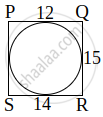
Explanation:
A quadrilateral PQRS is drawn to circumscribe a circle.
Hence,
PQ + RS = QR + SP
12 + 14 = 15 + SP
SP = 26 – 15
SP = 11 cm
APPEARS IN
संबंधित प्रश्न
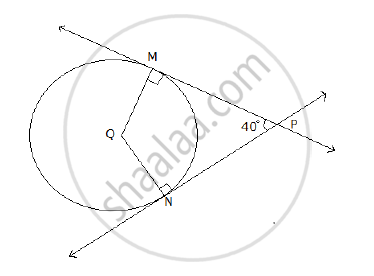
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
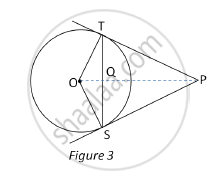
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
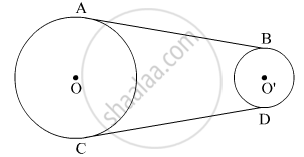
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
Find the area of the shaded region in Fig. 8, where \\

In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

The length of the tangent from an external point P on a circle with centre O is ______
In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
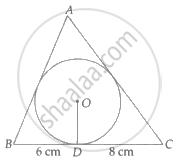
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. If the area of ΔABC is 84 cm2, find the lengths of sides AB and AC.
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
