Advertisements
Advertisements
प्रश्न
Equation of a circle which passes through (3, 6) and touches the axes is ______.
विकल्प
x2 + y2 + 6x + 6y + 3 = 0
x2 + y2 – 6x – 6y – 9 = 0
x2 + y2 – 6x – 6y + 9 = 0
None of these
उत्तर
Equation of a circle which passes through (3, 6) and touches the axes is x2 + y2 – 6x – 6y + 9 = 0.
Explanation: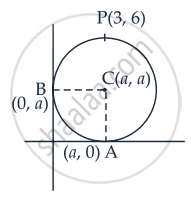
Let the required circle touch the axes at (a, 0) and (0, a)
∴ Centre is (a, a) and r = a
So the equation of the circle is (x – a)2 + (y – a)2 = a2
If it passes through a point P(3, 6) then
(3 – a)2 + (6 – a)2 = a2
⇒ 9 + a2 – 6a + 36 + a2 – 12a = a2
⇒ a2 – 18a + 45 = 0
⇒ a2 – 15a – 3a + 45 = 0
⇒ a(a – 15) – 3(a – 15) = 0
⇒ (a – 3)(a – 15) = 0
⇒ a = 3 and a = 15 which is not possible
∴ a = 3
So, the required equation of the circle is (x – 3)2 + (y – 3)2 = 9
⇒ x2 + 9 – 6x + y2 + 9 – 6y = 9
⇒ x2 + y2 – 6x – 6y + 9 = 0
APPEARS IN
संबंधित प्रश्न
Find the equation of the circle with:
Centre (a, b) and radius\[\sqrt{a^2 + b^2}\]
Find the equation of the circle with:
Centre (a cos α, a sin α) and radius a.
Find the equation of the circle with:
Centre (a, a) and radius \[\sqrt{2}\]a.
Find the centre and radius of each of the following circles:
(x + 5)2 + (y + 1)2 = 9
If the equations of two diameters of a circle are 2x + y = 6 and 3x + 2y = 4 and the radius is 10, find the equation of the circle.
A circle whose centre is the point of intersection of the lines 2x − 3y + 4 = 0 and 3x + 4y− 5 = 0 passes through the origin. Find its equation.
Find the equations of the circles passing through two points on Y-axis at distances 3 from the origin and having radius 5.
If the lines 2x − 3y = 5 and 3x − 4y = 7 are the diameters of a circle of area 154 square units, then obtain the equation of the circle.
Find the equation of the circle having (1, −2) as its centre and passing through the intersection of the lines 3x + y = 14 and 2x + 5y = 18.
If the lines 3x − 4y + 4 = 0 and 6x − 8y − 7 = 0 are tangents to a circle, then find the radius of the circle.
If the line 2x − y + 1 = 0 touches the circle at the point (2, 5) and the centre of the circle lies on the line x + y − 9 = 0. Find the equation of the circle.
Find the equation of the circle concentric with x2 + y2 − 4x − 6y − 3 = 0 and which touches the y-axis.
Find the equation of the circle, the end points of whose diameter are (2, −3) and (−2, 4). Find its centre and radius.
Find the equation of the circle passing through the origin and the points where the line 3x + 4y = 12 meets the axes of coordinates.
Find the equation of the circle which passes through the origin and cuts off intercepts aand b respectively from x and y - axes.
The abscissae of the two points A and B are the roots of the equation x2 + 2ax − b2 = 0 and their ordinates are the roots of the equation x2 + 2px − q2 = 0. Find the equation of the circle with AB as diameter. Also, find its radius.
ABCD is a square whose side is a; taking AB and AD as axes, prove that the equation of the circle circumscribing the square is x2 + y2 − a (x + y) = 0.
If the equation of a circle is λx2 + (2λ − 3) y2 − 4x + 6y − 1 = 0, then the coordinates of centre are
The radius of the circle represented by the equation 3x2 + 3y2 + λxy + 9x + (λ − 6) y + 3 = 0 is
The number of integral values of λ for which the equation x2 + y2 + λx + (1 − λ) y + 5 = 0 is the equation of a circle whose radius cannot exceed 5, is
The equation of the circle passing through the point (1, 1) and having two diameters along the pair of lines x2 − y2 −2x + 4y − 3 = 0, is
The equation of the circle passing through the origin which cuts off intercept of length 6 and 8 from the axes is
The equation of the circle concentric with x2 + y2 − 3x + 4y − c = 0 and passing through (−1, −2) is
The area of an equilateral triangle inscribed in the circle x2 + y2 − 6x − 8y − 25 = 0 is
The equation of the circle which touches the axes of coordinates and the line \[\frac{x}{3} + \frac{y}{4} = 1\] and whose centres lie in the first quadrant is x2 + y2 − 2cx − 2cy + c2 = 0, where c is equal to
If (x, 3) and (3, 5) are the extremities of a diameter of a circle with centre at (2, y), then the values of x and y are
Equation of the circle through origin which cuts intercepts of length a and b on axes is
The equation of the circle circumscribing the triangle whose sides are the lines y = x + 2, 3y = 4x, 2y = 3x is ______.
