Question

The area of an equilateral triangle inscribed in the circle x² + y² − 6x − 8y − 25 = 0 is

विकल्प

• \[\frac{225\sqrt{3}}{6}\]

•  25π

• 50π − 100

• none of these

Answer 1

\[\frac{225\sqrt{3}}{6}\]

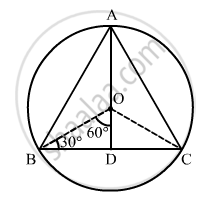
Let ABC be the required equilateral triangle.
The equation of the circle is x² + y² − 6x − 8y − 25 = 0.
Therefore, coordinates of the centre O is \[\left( 3, 4 \right)\].

Radius of the circle = OA = OB = OC = \[\sqrt{9 + 16 + 25} = 5\sqrt{2}\] 

In  \[∆\] BOD, we have:

\[\sin60° = \frac{DB}{BO}\]

\[ \Rightarrow DB = \frac{\sqrt{3}}{2}\left( 5\sqrt{2} \right)\]

\[ \Rightarrow BC = 2BD = \sqrt{3}\left( 5\sqrt{2} \right) = 5\sqrt{6}\]

Now, area of \[\bigtriangleup ABC\] = \[\frac{\sqrt{3}}{4}B C^2 = \frac{\sqrt{3}}{4} \left( 5\sqrt{6} \right)^2 = \frac{\sqrt{3}\left( 150 \right)}{4} = \frac{\sqrt{3}\left( 75 \right)}{2} = \frac{\sqrt{3}\left( 225 \right)}{6}\]

square units