Advertisements
Advertisements
प्रश्न
Equation of the circle with centre on the y-axis and passing through the origin and the point (2, 3) is ______.
विकल्प
x2 + y2 + 13y = 0
3x2 + 3y2 + 13x + 3 = 0
6x2 + 6y2 – 13x = 0
x2 + y2 + 13x + 3 = 0
Advertisements
उत्तर
Equation of the circle with centre on the y-axis and passing through the origin and the point (2, 3) is x2 + y2 + 13y = 0.
Explanation: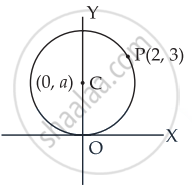
Let the equation of the circle be (x – h)2 + (y – k)2 = r2
Let the centre be (0, a)
∴ Radius r = a
So, the equation of the circle is (x – 0)2 + (y – a)2 = a2
⇒ x2 + (y – a)2 = a2
⇒ x2 + y2 + a2 – 2ay = a2
⇒ x2 + y2 – 2ay = 0 ......(i)
Now CP = r
⇒ `sqrt((2 - 0)^2 + (3 - a)^2) = a`
⇒ `sqrt(4 + 9 + a^2 - 6a) = a`
⇒ `sqrt(13 + a^2 - 6a) = a`
⇒ `13 + a^2 - 6a = a^2`
⇒ `13 - 6a = 0`
∴ `a = 13/6`
Putting the value of a in equation (i) we get
`x^2 + y^2 - 2(13/6)y` = 0
⇒ 3x2 + 3y2 – 13y = 0
APPEARS IN
संबंधित प्रश्न
Find the centre and radius of each of the following circles:
x2 + y2 − 4x + 6y = 5
Find the centre and radius of each of the following circles:
x2 + y2 − x + 2y − 3 = 0.
Find the equation of the circle whose centre is (1, 2) and which passes through the point (4, 6).
Find the equation of the circle passing through the point of intersection of the lines x + 3y = 0 and 2x − 7y = 0 and whose centre is the point of intersection of the lines x + y + 1 = 0 and x − 2y + 4 = 0.
Find the equation of a circle
passing through the origin, radius 17 and ordinate of the centre is −15.
If the line y = \[\sqrt{3}\] x + k touches the circle x2 + y2 = 16, then find the value of k.
Find the equation of the circle having (1, −2) as its centre and passing through the intersection of the lines 3x + y = 14 and 2x + 5y = 18.
Show that the point (x, y) given by \[x = \frac{2at}{1 + t^2}\] and \[y = a\left( \frac{1 - t^2}{1 + t^2} \right)\] lies on a circle for all real values of t such that \[- 1 \leq t \leq 1\] where a is any given real number.
Find the coordinates of the centre and radius of each of the following circles: 2x2 + 2y2 − 3x + 5y = 7
Find the coordinates of the centre and radius of the following circle:
1/2 (x2 + y2) + x cos θ + y sin θ − 4 = 0
Find the equation of the circle which passes through (3, −2), (−2, 0) and has its centre on the line 2x − y = 3.
Show that the points (5, 5), (6, 4), (−2, 4) and (7, 1) all lie on a circle, and find its equation, centre and radius.
Find the equation of the circle which circumscribes the triangle formed by the lines x + y + 3 = 0, x − y + 1 = 0 and x = 3
Find the equation of the circle which circumscribes the triangle formed by the lines y = x + 2, 3y = 4x and 2y = 3x.
Find the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the positive side of the x-axis and y-axis respectively.
Find the equation of the circle concentric with the circle x2 + y2 − 6x + 12y + 15 = 0 and double of its area.
Find the equation to the circle which passes through the points (1, 1) (2, 2) and whose radius is 1. Show that there are two such circles.
Find the equation of the circle the end points of whose diameter are the centres of the circles x2 + y2 + 6x − 14y − 1 = 0 and x2 + y2 − 4x + 10y − 2 = 0.
Find the equation of the circle circumscribing the rectangle whose sides are x − 3y = 4, 3x + y = 22, x − 3y = 14 and 3x + y = 62.
Find the equation of the circle which passes through the origin and cuts off intercepts aand b respectively from x and y - axes.
Find the equation of the circle whose diameter is the line segment joining (−4, 3) and (12, −1). Find also the intercept made by it on y-axis.
The line 2x − y + 6 = 0 meets the circle x2 + y2 − 2y − 9 = 0 at A and B. Find the equation of the circle on AB as diameter.
Find the equations of the circles which pass through the origin and cut off equal chords of \[\sqrt{2}\] units from the lines y = x and y = − x.
If the abscissae and ordinates of two points P and Q are roots of the equations x2 + 2ax − b2 = 0 and x2 + 2px − q2 = 0 respectively, then write the equation of the circle with PQ as diameter.
Write the equation of the unit circle concentric with x2 + y2 − 8x + 4y − 8 = 0.
The equation x2 + y2 + 2x − 4y + 5 = 0 represents
If the point (2, k) lies outside the circles x2 + y2 + x − 2y − 14 = 0 and x2 + y2 = 13 then k lies in the interval
If the point (λ, λ + 1) lies inside the region bounded by the curve \[x = \sqrt{25 - y^2}\] and y-axis, then λ belongs to the interval
If the circles x2 + y2 = 9 and x2 + y2 + 8y + c = 0 touch each other, then c is equal to
The equation of the circle concentric with x2 + y2 − 3x + 4y − c = 0 and passing through (−1, −2) is
The circle x2 + y2 + 2gx + 2fy + c = 0 does not intersect x-axis, if
The equation of the circle which touches the axes of coordinates and the line \[\frac{x}{3} + \frac{y}{4} = 1\] and whose centres lie in the first quadrant is x2 + y2 − 2cx − 2cy + c2 = 0, where c is equal to
If (x, 3) and (3, 5) are the extremities of a diameter of a circle with centre at (2, y), then the values of x and y are
If (−3, 2) lies on the circle x2 + y2 + 2gx + 2fy + c = 0 which is concentric with the circle x2 + y2 + 6x + 8y − 5 = 0, then c =
