Advertisements
Advertisements
प्रश्न
Equation of the circle with centre on the y-axis and passing through the origin and the point (2, 3) is ______.
पर्याय
x2 + y2 + 13y = 0
3x2 + 3y2 + 13x + 3 = 0
6x2 + 6y2 – 13x = 0
x2 + y2 + 13x + 3 = 0
उत्तर
Equation of the circle with centre on the y-axis and passing through the origin and the point (2, 3) is x2 + y2 + 13y = 0.
Explanation: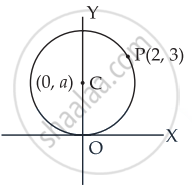
Let the equation of the circle be (x – h)2 + (y – k)2 = r2
Let the centre be (0, a)
∴ Radius r = a
So, the equation of the circle is (x – 0)2 + (y – a)2 = a2
⇒ x2 + (y – a)2 = a2
⇒ x2 + y2 + a2 – 2ay = a2
⇒ x2 + y2 – 2ay = 0 ......(i)
Now CP = r
⇒ `sqrt((2 - 0)^2 + (3 - a)^2) = a`
⇒ `sqrt(4 + 9 + a^2 - 6a) = a`
⇒ `sqrt(13 + a^2 - 6a) = a`
⇒ `13 + a^2 - 6a = a^2`
⇒ `13 - 6a = 0`
∴ `a = 13/6`
Putting the value of a in equation (i) we get
`x^2 + y^2 - 2(13/6)y` = 0
⇒ 3x2 + 3y2 – 13y = 0
APPEARS IN
संबंधित प्रश्न
Find the centre and radius of each of the following circles:
(x + 5)2 + (y + 1)2 = 9
Find the centre and radius of each of the following circles:
x2 + y2 − x + 2y − 3 = 0.
Find the equation of the circle passing through the point of intersection of the lines x + 3y = 0 and 2x − 7y = 0 and whose centre is the point of intersection of the lines x + y + 1 = 0 and x − 2y + 4 = 0.
Find the equation of the circle whose centre lies on the positive direction of y - axis at a distance 6 from the origin and whose radius is 4.
If the equations of two diameters of a circle are 2x + y = 6 and 3x + 2y = 4 and the radius is 10, find the equation of the circle.
Find the equation of a circle
passing through the origin, radius 17 and ordinate of the centre is −15.
A circle whose centre is the point of intersection of the lines 2x − 3y + 4 = 0 and 3x + 4y− 5 = 0 passes through the origin. Find its equation.
A circle of radius 4 units touches the coordinate axes in the first quadrant. Find the equations of its images with respect to the line mirrors x = 0 and y = 0.
Find the equations of the circles touching y-axis at (0, 3) and making an intercept of 8 units on the X-axis.
Find the equations of the circles passing through two points on Y-axis at distances 3 from the origin and having radius 5.
Show that the point (x, y) given by \[x = \frac{2at}{1 + t^2}\] and \[y = a\left( \frac{1 - t^2}{1 + t^2} \right)\] lies on a circle for all real values of t such that \[- 1 \leq t \leq 1\] where a is any given real number.
If the line 2x − y + 1 = 0 touches the circle at the point (2, 5) and the centre of the circle lies on the line x + y − 9 = 0. Find the equation of the circle.
Show that the points (3, −2), (1, 0), (−1, −2) and (1, −4) are concyclic.
Show that the points (5, 5), (6, 4), (−2, 4) and (7, 1) all lie on a circle, and find its equation, centre and radius.
Find the equation of the circle which circumscribes the triangle formed by the lines y = x + 2, 3y = 4x and 2y = 3x.
Prove that the radii of the circles x2 + y2 = 1, x2 + y2 − 2x − 6y − 6 = 0 and x2 + y2 − 4x − 12y − 9 = 0 are in A.P.
The sides of a square are x = 6, x = 9, y = 3 and y = 6. Find the equation of a circle drawn on the diagonal of the square as its diameter.
Find the equations of the circles which pass through the origin and cut off equal chords of \[\sqrt{2}\] units from the lines y = x and y = − x.
If the radius of the circle x2 + y2 + ax + (1 − a) y + 5 = 0 does not exceed 5, write the number of integral values a.
If the circles x2 + y2 = 9 and x2 + y2 + 8y + c = 0 touch each other, then c is equal to
The equation of a circle with radius 5 and touching both the coordinate axes is
The equation of the circle concentric with x2 + y2 − 3x + 4y − c = 0 and passing through (−1, −2) is
The circle x2 + y2 + 2gx + 2fy + c = 0 does not intersect x-axis, if
The equation of the circle which touches the axes of coordinates and the line \[\frac{x}{3} + \frac{y}{4} = 1\] and whose centres lie in the first quadrant is x2 + y2 − 2cx − 2cy + c2 = 0, where c is equal to
Equation of the circle through origin which cuts intercepts of length a and b on axes is
The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is ______.
