Advertisements
Advertisements
प्रश्न
Find the equation of the parabola whose focus is the point (2, 3) and directrix is the line x − 4y + 3 = 0. Also, find the length of its latus-rectum.
उत्तर
Let P (x, y) be any point on the parabola whose focus is S (2, 3) and the directrix is x − 4y+ 3 = 0.
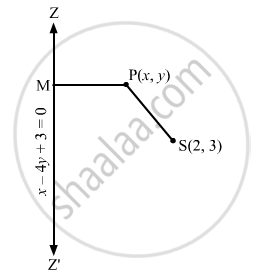
Draw PM perpendicular to x − 4y + 3=0.
Then, we have:
\[SP = PM\]
\[ \Rightarrow S P^2 = P M^2 \]
\[ \Rightarrow \left( x - 2 \right)^2 + \left( y - 3 \right)^2 = \left( \frac{x - 4y + 3}{\sqrt{1 + 16}} \right)^2 \]
\[ \Rightarrow \left( x - 2 \right)^2 + \left( y - 3 \right)^2 = \left( \frac{x - 4y + 3}{\sqrt{17}} \right)^2 \]
\[ \Rightarrow 17\left( x^2 + 4 - 4x + y^2 - 6y + 9 \right) = x^2 + 16 y^2 + 9 - 8xy - 24y + 6x\]
\[ \Rightarrow \left( 17 x^2 - 68x + 17 y^2 - 102y + 13 \times 17 \right) = x^2 + 16 y^2 + 9 - 8xy - 24y + 6x\]
\[ \Rightarrow 16 x^2 + y^2 + 8xy - 74x - 78y + 212 = 0\]
Length of the latus rectum = 2(Length of the perpendicular from the focus on the directrix)
= 2(Length of the perpendicular from (2, 3) on the directrix)
=\[2\left| \frac{2 - 12 + 3}{\sqrt{16 + 1}} \right| = 2\left| \frac{- 7}{\sqrt{17}} \right| = 2\left( \frac{7}{\sqrt{17}} \right) = \frac{14}{\sqrt{17}}\]
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
y2 = – 8x
Find the equation of the parabola that satisfies the following condition:
Focus (6, 0); directrix x = –6
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0); focus (3, 0)
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0) focus (–2, 0)
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0) passing through (2, 3) and axis is along x-axis
If a parabolic reflector is 20 cm in diameter and 5 cm deep, find the focus.
An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?
The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
Find the equation of the parabola if
the focus is at (−6, −6) and the vertex is at (−2, 2)
Find the equation of the parabola if the focus is at (0, −3) and the vertex is at (−1, −3)
Find the equation of the parabola if the focus is at (a, 0) and the vertex is at (a', 0)
Find the equation of a parabola with vertex at the origin, the axis along x-axis and passing through (2, 3).
Find the equation of a parabola with vertex at the origin and the directrix, y = 2.
Find the equation of the parabola whose focus is (5, 2) and having vertex at (3, 2).
Find the equations of the lines joining the vertex of the parabola y2 = 6x to the point on it which have abscissa 24.
Find the coordinates of points on the parabola y2 = 8x whose focal distance is 4.
If the line y = mx + 1 is tangent to the parabola y2 = 4x, then find the value of m.
Write the equation of the directrix of the parabola x2 − 4x − 8y + 12 = 0.
Write the equation of the parabola with focus (0, 0) and directrix x + y − 4 = 0.
PSQ is a focal chord of the parabola y2 = 8x. If SP = 6, then write SQ.
The equation of the parabola whose vertex is (a, 0) and the directrix has the equation x + y = 3a, is
The parametric equations of a parabola are x = t2 + 1, y = 2t + 1. The cartesian equation of its directrix is
The line 2x − y + 4 = 0 cuts the parabola y2 = 8x in P and Q. The mid-point of PQ is
The equation 16x2 + y2 + 8xy − 74x − 78y + 212 = 0 represents
The locus of the points of trisection of the double ordinates of a parabola is a
The equations of the lines joining the vertex of the parabola y2 = 6x to the points on it which have abscissa 24 are ______.
If the line y = mx + 1 is tangent to the parabola y2 = 4x then find the value of m.
Find the equation of the following parabolas:
Directrix x = 0, focus at (6, 0)
