Advertisements
Advertisements
प्रश्न
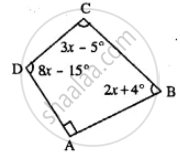
From the following figure find;
- x
- ∠ABC
- ∠ACD
उत्तर
(i) In Quadrilateral ABCD,
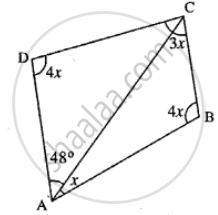
x + 4x + 3x + 4x + 48° = 360°
12x = 360° – 48°
12x = 312
x = `312/12` = 26°
(ii) ∠ABC = 4x
4 × 26 = 104°
(iii) ∠ACD = 180° − 4x − 48°
= 180° − 4 × 26° − 48°
= 180° − 104° − 48°
= 180° − 152° = 28°
APPEARS IN
संबंधित प्रश्न
Given here are some figures:
 |
 |
 |
 |
 |
 |
 |
 |
Classify each of them on the basis of the following:
- Simple curve
- Simple closed curve
- Polygon
- Convex polygon
- Concave polygon
Complete of the following, so as to make a true statement:
A quadrilateral has .... diagonals.
Complete of the following, so as to make a true statement:
In a quadrilateral the point of intersection of the diagonals lies in .... of the quadrilateral.
Complete of the following, so as to make a true statement:
A point is in the interior of a convex quadrilateral, if it is in the ..... of its two opposite angles.
A quadrilateral has all its four angles of the same measure. What is the measure of each?
If the sum of the two angles of a quadrilateral is 180°. What is the sum of the remaining two angles?
Complete the following statement by means of one of those given in brackets against each:
If one pair of opposite sides are equal and parallel, then the figure is ........................
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and the respectively. If AB = 12 cm, MN = 14 cm, then CD =
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ; ∠A = 5(a+2)° and ∠B = 2(2a+7)°.
Calculate ∠A.
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
In parallelogram ABCD, ∠A = 90°
(i) What is the measure of angle B.
(ii) Write the special name of the parallelogram.
Observe the figure below and find out their name.
The three angles of a quadrilateral are 71°, 110°, 95°. Find its fourth angle.
One angle of a hexagon is 140° and the remaining angles are in the ratio 4 : 3 : 4 : 5 : 4. Calculate the measures of the smallest and the largest angles.
ABCDE is a pentagon in which AB is parallel to DC and ∠A : ∠E : ∠D = 1 : 2 : 3. Find angle A.
If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a ______.
In quadrilateral ROPE, the pairs of adjacent angles are ______.
In figure, ∠XYZ cannot be written as ______.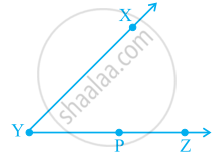
In the given figure.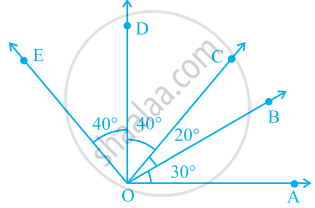
∠AOD is a/an ____ angle
In given figure, name any four angles that appear to be acute angles.
In given figure, What is BD – BE?
Using the information given, name the right angles in part of figure:
AE ⊥ CE
What conclusion can be drawn from part of given figure, if DB is the bisector of ∠ADC?
Draw a rough sketch of a quadrilateral KLMN. State two pairs of opposite angles.
Investigate :
Use strips and fasteners to make a triangle and a quadrilateral.
Try to push inward at any one vertex of the triangle. Do the same to the quadrilateral. Is the triangle distorted? Is the quadrilateral distorted? Is the triangle rigid?
Why is it that structures like electric towers make use of triangular shapes and not quadrilaterals?
