Advertisements
Advertisements
प्रश्न
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`x^2/25 - y^2/144` = 1
उत्तर
It is Hyperbola.
The transverse axis the x-axis.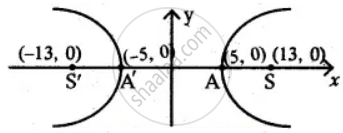
a2 = 25, b2 = 144
a = 5, b = 12
c2 = a2 + b2
= 25 + 144
= 169
c = 13
ae = 13
5e = 13
e = `13/5`
(a) Centre (0, 0)
(b) Vertex (± a, 0) = (± 5, 0)
(c) Foci (± c, 0) = (± 13, 0)
(d) Equation of the directrix
x = `+- "a"/"e" = +- 5/(13/5) = +- 25/13`
x = `+- 25/13`
APPEARS IN
संबंधित प्रश्न
Find the equation of the parabola which is symmetrical about x-axis and passing through (–2, –3).
The focus of the parabola x2 = 16y is:
The double ordinate passing through the focus is:
The equation of directrix of the parabola y2 = -x is:
Find the equation of the parabola in the cases given below:
Vertex (1, – 2) and Focus (4, – 2)
Find the equation of the ellipse in the cases given below:
Foci `(+- 3, 0), "e"+ 1/2`
Find the equation of the ellipse in the cases given below:
Length of latus rectum 8, eccentricity = `3/5` centre (0, 0) and major axis on x-axis
Find the equation of the hyperbola in the cases given below:
Foci (± 2, 0), Eccentricity = `3/2`
Find the equation of the hyperbola in the cases given below:
Centre (2, 1), one of the foci (8, 1) and corresponding directrix x = 4
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
x2 = 24y
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
y2 = – 8x
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
x2 – 2x + 8y + 17 = 0
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`x^2/25 + y^2/9` = 1
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`y^2/16 - x^2/9` = 1
Prove that the length of the latus rectum of the hyperbola `x^2/"a"^2 - y^2/"b"^2` = 1 is `(2"b"^2)/"a"`
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`(x - 3)^2/225 + (y - 4)^2/289` = 1
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
`(x + 1)^2/100 + (y - 2)^2/64` = 1
Identify the type of conic and find centre, foci, vertices, and directrices of the following:
9x2 – y2 – 36x – 6y + 18 = 0
Choose the correct alternative:
The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half the distance between the foci is
