Advertisements
Advertisements
प्रश्न
If the foot of perpendicular drawn from the origin to a plane is (5, – 3, – 2), then the equation of plane is `vecr.(5hati - 3hatj - 2hatk)` = 38.
विकल्प
True
False
उत्तर
This statement is True.
Explanation:
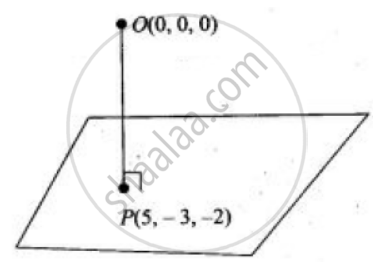
From the figure normal to the plane is `vecn = vec(OP) = 5hati - 3hatj - 2hatk`
Plane passing through the point P(5, – 3, – 2).
∴ Equation of the plane is `5(x - 5) - 3(y + 3) - 2(z + 2)` = 0
or `5x - 3y - 2z` = 38
APPEARS IN
संबंधित प्रश्न
Coordinate planes divide the space into ______ octants.
Name the octants in which the following points lie:
(–5, 4, 3)
Find the image of:
(–2, 3, 4) in the yz-plane.
Find the distances of the point P(–4, 3, 5) from the coordinate axes.
Show that the points (a, b, c), (b, c, a) and (c, a, b) are the vertices of an equilateral triangle.
Verify the following:
(0, 7, –10), (1, 6, –6) and (4, 9, –6) are vertices of an isosceles triangle.
Verify the following:
(0, 7, –10), (1, 6, –6) and (4, 9, –6) are vertices of an isosceles triangle.
Verify the following:
(–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are vertices of a parallelogram.
Show that the points A(1, 2, 3), B(–1, –2, –1), C(2, 3, 2) and D(4, 7, 6) are the vertices of a parallelogram ABCD, but not a rectangle.
Find the equation of the set of the points P such that its distances from the points A(3, 4, –5) and B(–2, 1, 4) are equal.
Write the distance of the point P (2, 3,5) from the xy-plane.
XOZ-plane divides the join of (2, 3, 1) and (6, 7, 1) in the ratio
The coordinates of the foot of the perpendicular from a point P(6,7, 8) on x - axis are
The perpendicular distance of the point P (6, 7, 8) from xy - plane is
The perpendicular distance of the point P(3, 3,4) from the x-axis is
If the direction ratios of a line are 1, 1, 2, find the direction cosines of the line.
Find the coordinates of the point where the line through (3, – 4, – 5) and (2, –3, 1) crosses the plane passing through three points (2, 2, 1), (3, 0, 1) and (4, –1, 0)
Find the image of the point having position vector `hati + 3hatj + 4hatk` in the plane `hatr * (2hati - hatj + hatk)` + 3 = 0.
A line makes equal angles with co-ordinate axis. Direction cosines of this line are ______.
If a line makes angles `pi/2, 3/4 pi` and `pi/4` with x, y, z axis, respectively, then its direction cosines are ______.
Find the equation of the plane through the points (2, 1, 0), (3, –2, –2) and (3, 1, 7).
Two systems of rectangular axis have the same origin. If a plane cuts them at distances a, b, c and a′, b′, c′, respectively, from the origin, prove that
`1/a^2 + 1/b^2 + 1/c^2 = 1/(a"'"^2) + 1/(b"'"^2) + 1/(c"'"^2)`
Find the equation of the plane through the points (2, 1, –1) and (–1, 3, 4), and perpendicular to the plane x – 2y + 4z = 10.
The locus represented by xy + yz = 0 is ______.
The plane 2x – 3y + 6z – 11 = 0 makes an angle sin–1(α) with x-axis. The value of α is equal to ______.
The unit vector normal to the plane x + 2y +3z – 6 = 0 is `1/sqrt(14)hati + 2/sqrt(14)hatj + 3/sqrt(14)hatk`.
The angle between the line `vecr = (5hati - hatj - 4hatk) + lambda(2hati - hatj + hatk)` and the plane `vec.(3hati - 4hatj - hatk)` + 5 = 0 is `sin^-1(5/(2sqrt(91)))`.
The angle between the planes `vecr.(2hati - 3hatj + hatk)` = 1 and `vecr.(hati - hatj)` = 4 is `cos^-1((-5)/sqrt(58))`.
