Advertisements
Advertisements
प्रश्न
Find the distances of the point P(–4, 3, 5) from the coordinate axes.
Advertisements
उत्तर
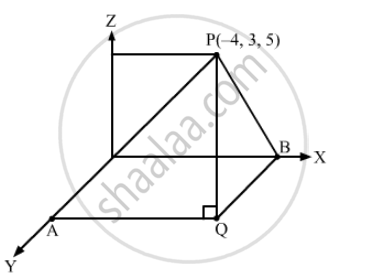
Let PQ be the perpendicular to the xy-plane and QA be perpendicular from Q to the y-axis.
PA will be perpendicular to the x-axis.
Also, QA = \[\left| 3 \right|\]and PQ =\[\left| 5 \right|\]
Now, distance of P from the x-axis:
PB =\[\sqrt{B Q^2 + Q P^2}\]
\[= \sqrt{3^2 + 5^2}\]
\[ = \sqrt{9 + 25} = \sqrt{34}\]
Similarly,
From the right-angled \[∆ PAQ\]distance of P from the y-axis:
PA =\[\sqrt{A Q^2 + Q P^2}\]
\[ = \sqrt{16 + 25} = \sqrt{41}\]
\[ = \sqrt{25} = 5\]
APPEARS IN
संबंधित प्रश्न
Three vertices of a parallelogram ABCD are A (3, –1, 2), B (1, 2, –4) and C (–1, 1, 2). Find the coordinates of the fourth vertex.
Name the octants in which the following points lie: (5, 2, 3)
Name the octants in which the following points lie:
(4, –3, 5)
Name the octants in which the following points lie:
(–5, –4, 7)
Find the image of:
(–5, 4, –3) in the xz-plane.
Find the image of:
(–5, 0, 3) in the xz-plane.
Find the image of:
(–4, 0, 0) in the xy-plane.
A cube of side 5 has one vertex at the point (1, 0, –1), and the three edges from this vertex are, respectively, parallel to the negative x and y axes and positive z-axis. Find the coordinates of the other vertices of the cube.
Planes are drawn through the points (5, 0, 2) and (3, –2, 5) parallel to the coordinate planes. Find the lengths of the edges of the rectangular parallelepiped so formed.
Determine the point on z-axis which is equidistant from the points (1, 5, 7) and (5, 1, –4).
Find the points on z-axis which are at a distance \[\sqrt{21}\]from the point (1, 2, 3).
Prove that the triangle formed by joining the three points whose coordinates are (1, 2, 3), (2, 3, 1) and (3, 1, 2) is an equilateral triangle.
Show that the points (a, b, c), (b, c, a) and (c, a, b) are the vertices of an equilateral triangle.
Verify the following:
(0, 7, –10), (1, 6, –6) and (4, 9, –6) are vertices of an isosceles triangle.
Verify the following:
(–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are vertices of a parallelogram.
Verify the following:
(5, –1, 1), (7, –4,7), (1, –6,10) and (–1, – 3,4) are the vertices of a rhombus.
Find the locus of the points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
Find the locus of the point, the sum of whose distances from the points A(4, 0, 0) and B(–4, 0, 0) is equal to 10.
Show that the points A(1, 2, 3), B(–1, –2, –1), C(2, 3, 2) and D(4, 7, 6) are the vertices of a parallelogram ABCD, but not a rectangle.
Find the ratio in which the sphere x2 + y2 + z2 = 504 divides the line joining the points (12, –4, 8) and (27, –9, 18).
The perpendicular distance of the point P (6, 7, 8) from xy - plane is
The length of the perpendicular drawn from the point P(a, b, c) from z-axis is
If a line makes an angle of 30°, 60°, 90° with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
Find the coordinates of the point where the line through (3, – 4, – 5) and (2, –3, 1) crosses the plane passing through three points (2, 2, 1), (3, 0, 1) and (4, –1, 0)
If a line makes angles `pi/2, 3/4 pi` and `pi/4` with x, y, z axis, respectively, then its direction cosines are ______.
If a line makes an angle of `pi/4` with each of y and z axis, then the angle which it makes with x-axis is ______.
Find the equation of a plane which bisects perpendicularly the line joining the points A(2, 3, 4) and B(4, 5, 8) at right angles.
Find the equations of the two lines through the origin which intersect the line `(x - 3)/2 = (y - 3)/1 = z/1` at angles of `pi/3` each.
Find the angle between the lines whose direction cosines are given by the equations l + m + n = 0, l2 + m2 – n2 = 0
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
The plane ax + by = 0 is rotated about its line of intersection with the plane z = 0 through an angle α. Prove that the equation of the plane in its new position is ax + by `+- (sqrt(a^2 + b^2) tan alpha)z ` = 0
The plane 2x – 3y + 6z – 11 = 0 makes an angle sin–1(α) with x-axis. The value of α is equal to ______.
The intercepts made by the plane 2x – 3y + 5z +4 = 0 on the co-ordinate axis are `-2, 4/3, - 4/5`.
The angle between the line `vecr = (5hati - hatj - 4hatk) + lambda(2hati - hatj + hatk)` and the plane `vec.(3hati - 4hatj - hatk)` + 5 = 0 is `sin^-1(5/(2sqrt(91)))`.
The vector equation of the line `(x - 5)/3 = (y + 4)/7 = (z - 6)/2` is `vecr = (5hati - 4hatj + 6hatk) + lambda(3hati + 7hatj - 2hatk)`.
If the foot of perpendicular drawn from the origin to a plane is (5, – 3, – 2), then the equation of plane is `vecr.(5hati - 3hatj - 2hatk)` = 38.
