Advertisements
Advertisements
प्रश्न
Find the distances of the point P(–4, 3, 5) from the coordinate axes.
उत्तर
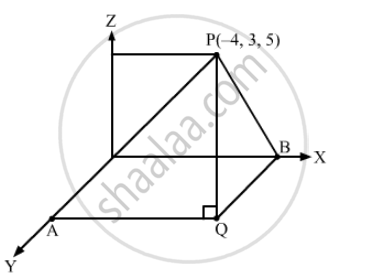
Let PQ be the perpendicular to the xy-plane and QA be perpendicular from Q to the y-axis.
PA will be perpendicular to the x-axis.
Also, QA = \[\left| 3 \right|\]and PQ =\[\left| 5 \right|\]
Now, distance of P from the x-axis:
PB =\[\sqrt{B Q^2 + Q P^2}\]
\[= \sqrt{3^2 + 5^2}\]
\[ = \sqrt{9 + 25} = \sqrt{34}\]
Similarly,
From the right-angled \[∆ PAQ\]distance of P from the y-axis:
PA =\[\sqrt{A Q^2 + Q P^2}\]
\[ = \sqrt{16 + 25} = \sqrt{41}\]
\[ = \sqrt{25} = 5\]
APPEARS IN
संबंधित प्रश्न
Coordinate planes divide the space into ______ octants.
If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (–4, 3b, –10) and R (8, 14, 2c), then find the values of a, b and c.
Name the octants in which the following points lie:
(4, –3, 5)
Name the octants in which the following points lie:
(7, 4, –3)
Name the octants in which the following points lie:
(–5, –4, 7)
Find the image of:
(–2, 3, 4) in the yz-plane.
Find the image of:
(–5, 4, –3) in the xz-plane.
Find the image of:
(5, 2, –7) in the xy-plane.
Find the image of:
(–5, 0, 3) in the xz-plane.
Determine the points in zx-plane are equidistant from the points A(1, –1, 0), B(2, 1, 2) and C(3, 2, –1).
Show that the points A(3, 3, 3), B(0, 6, 3), C(1, 7, 7) and D(4, 4, 7) are the vertices of a square.
Find the locus of P if PA2 + PB2 = 2k2, where A and B are the points (3, 4, 5) and (–1, 3, –7).
Verify the following:
(0, 7, 10), (–1, 6, 6) and (–4, 9, –6) are vertices of a right-angled triangle.
Find the locus of the points which are equidistant from the points (1, 2, 3) and (3, 2, –1).
Find the ratio in which the sphere x2 + y2 + z2 = 504 divides the line joining the points (12, –4, 8) and (27, –9, 18).
Show that the plane ax + by + cz + d = 0 divides the line joining the points (x1, y1, z1) and (x2, y2, z2) in the ratio \[- \frac{a x_1 + b y_1 + c z_1 + d}{a x_2 + b y_2 + c z_2 + d}\]
Write the distance of the point P (2, 3,5) from the xy-plane.
The ratio in which the line joining (2, 4, 5) and (3, 5, –9) is divided by the yz-plane is
The ratio in which the line joining the points (a, b, c) and (–a, –c, –b) is divided by the xy-plane is
The coordinates of the foot of the perpendicular from a point P(6,7, 8) on x - axis are
The length of the perpendicular drawn from the point P (3, 4, 5) on y-axis is
The perpendicular distance of the point P(3, 3,4) from the x-axis is
The length of the perpendicular drawn from the point P(a, b, c) from z-axis is
If the direction ratios of a line are 1, 1, 2, find the direction cosines of the line.
The x-coordinate of a point on the line joining the points Q(2, 2, 1) and R(5, 1, –2) is 4. Find its z-coordinate.
Find the coordinates of the point where the line through (3, – 4, – 5) and (2, –3, 1) crosses the plane passing through three points (2, 2, 1), (3, 0, 1) and (4, –1, 0)
Find the co-ordinates of the foot of perpendicular drawn from the point A(1, 8, 4) to the line joining the points B(0, –1, 3) and C(2, –3, –1).
Find the image of the point having position vector `hati + 3hatj + 4hatk` in the plane `hatr * (2hati - hatj + hatk)` + 3 = 0.
If a line makes angles α, β, γ with the positive directions of the coordinate axes, then the value of sin2α + sin2β + sin2γ is ______.
If a line makes an angle of `pi/4` with each of y and z axis, then the angle which it makes with x-axis is ______.
Find the equation of the plane through the points (2, 1, 0), (3, –2, –2) and (3, 1, 7).
If a variable line in two adjacent positions has direction cosines l, m, n and l + δl, m + δm, n + δn, show that the small angle δθ between the two positions is given by δθ2 = δl2 + δm2 + δn2
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
The vector equation of the line through the points (3, 4, –7) and (1, –1, 6) is ______.
The cartesian equation of the plane `vecr * (hati + hatj - hatk)` is ______.
The unit vector normal to the plane x + 2y +3z – 6 = 0 is `1/sqrt(14)hati + 2/sqrt(14)hatj + 3/sqrt(14)hatk`.
The intercepts made by the plane 2x – 3y + 5z +4 = 0 on the co-ordinate axis are `-2, 4/3, - 4/5`.
The line `vecr = 2hati - 3hatj - hatk + lambda(hati - hatj + 2hatk)` lies in the plane `vecr.(3hati + hatj - hatk) + 2` = 0.
