Advertisements
Advertisements
Question
Find the distances of the point P(–4, 3, 5) from the coordinate axes.
Solution
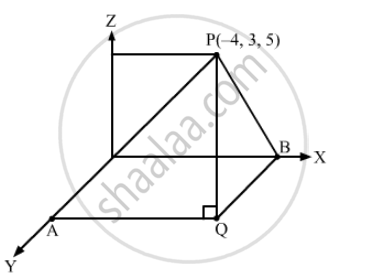
Let PQ be the perpendicular to the xy-plane and QA be perpendicular from Q to the y-axis.
PA will be perpendicular to the x-axis.
Also, QA = \[\left| 3 \right|\]and PQ =\[\left| 5 \right|\]
Now, distance of P from the x-axis:
PB =\[\sqrt{B Q^2 + Q P^2}\]
\[= \sqrt{3^2 + 5^2}\]
\[ = \sqrt{9 + 25} = \sqrt{34}\]
Similarly,
From the right-angled \[∆ PAQ\]distance of P from the y-axis:
PA =\[\sqrt{A Q^2 + Q P^2}\]
\[ = \sqrt{16 + 25} = \sqrt{41}\]
\[ = \sqrt{25} = 5\]
APPEARS IN
RELATED QUESTIONS
The x-axis and y-axis taken together determine a plane known as_______.
Name the octants in which the following points lie:
(–5, 4, 3)
Find the image of:
(–5, 4, –3) in the xz-plane.
A cube of side 5 has one vertex at the point (1, 0, –1), and the three edges from this vertex are, respectively, parallel to the negative x and y axes and positive z-axis. Find the coordinates of the other vertices of the cube.
Planes are drawn parallel to the coordinate planes through the points (3, 0, –1) and (–2, 5, 4). Find the lengths of the edges of the parallelepiped so formed.
Determine the points in zx-plane are equidistant from the points A(1, –1, 0), B(2, 1, 2) and C(3, 2, –1).
Find the points on z-axis which are at a distance \[\sqrt{21}\]from the point (1, 2, 3).
Prove that the point A(1, 3, 0), B(–5, 5, 2), C(–9, –1, 2) and D(–3, –3, 0) taken in order are the vertices of a parallelogram. Also, show that ABCD is not a rectangle.
If A(–2, 2, 3) and B(13, –3, 13) are two points.
Find the locus of a point P which moves in such a way the 3PA = 2PB.
Verify the following:
(–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are vertices of a parallelogram.
Show that the points A(1, 2, 3), B(–1, –2, –1), C(2, 3, 2) and D(4, 7, 6) are the vertices of a parallelogram ABCD, but not a rectangle.
Show that the plane ax + by + cz + d = 0 divides the line joining the points (x1, y1, z1) and (x2, y2, z2) in the ratio \[- \frac{a x_1 + b y_1 + c z_1 + d}{a x_2 + b y_2 + c z_2 + d}\]
Write the distance of the point P(3, 4, 5) from z-axis.
XOZ-plane divides the join of (2, 3, 1) and (6, 7, 1) in the ratio
What is the locus of a point for which y = 0, z = 0?
The length of the perpendicular drawn from the point P (3, 4, 5) on y-axis is
If the direction ratios of a line are 1, 1, 2, find the direction cosines of the line.
Find the direction cosines of the line passing through the points P(2, 3, 5) and Q(–1, 2, 4).
If a line makes an angle of 30°, 60°, 90° with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
The x-coordinate of a point on the line joining the points Q(2, 2, 1) and R(5, 1, –2) is 4. Find its z-coordinate.
A plane meets the co-ordinates axis in A, B, C such that the centroid of the ∆ABC is the point (α, β, γ). Show that the equation of the plane is `x/alpha + y/beta + z/γ` = 3
If α, β, γ are the angles that a line makes with the positive direction of x, y, z axis, respectively, then the direction cosines of the line are ______.
If a line makes angles α, β, γ with the positive directions of the coordinate axes, then the value of sin2α + sin2β + sin2γ is ______.
If the line drawn from the point (–2, – 1, – 3) meets a plane at right angle at the point (1, – 3, 3), find the equation of the plane
Find the equation of the plane through the points (2, 1, 0), (3, –2, –2) and (3, 1, 7).
Find the angle between the lines whose direction cosines are given by the equations l + m + n = 0, l2 + m2 – n2 = 0
If a variable line in two adjacent positions has direction cosines l, m, n and l + δl, m + δm, n + δn, show that the small angle δθ between the two positions is given by δθ2 = δl2 + δm2 + δn2
Find the length and the foot of perpendicular from the point `(1, 3/2, 2)` to the plane 2x – 2y + 4z + 5 = 0.
The plane ax + by = 0 is rotated about its line of intersection with the plane z = 0 through an angle α. Prove that the equation of the plane in its new position is ax + by `+- (sqrt(a^2 + b^2) tan alpha)z ` = 0
Show that the points `(hati - hatj + 3hatk)` and `3(hati + hatj + hatk)` are equidistant from the plane `vecr * (5hati + 2hatj - 7hatk) + 9` = 0 and lies on opposite side of it.
The area of the quadrilateral ABCD, where A(0, 4, 1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to ______.
The vector equation of the line through the points (3, 4, –7) and (1, –1, 6) is ______.
The unit vector normal to the plane x + 2y +3z – 6 = 0 is `1/sqrt(14)hati + 2/sqrt(14)hatj + 3/sqrt(14)hatk`.
The intercepts made by the plane 2x – 3y + 5z +4 = 0 on the co-ordinate axis are `-2, 4/3, - 4/5`.
The line `vecr = 2hati - 3hatj - hatk + lambda(hati - hatj + 2hatk)` lies in the plane `vecr.(3hati + hatj - hatk) + 2` = 0.
