Advertisements
Advertisements
Question
Planes are drawn through the points (5, 0, 2) and (3, –2, 5) parallel to the coordinate planes. Find the lengths of the edges of the rectangular parallelepiped so formed.
Solution
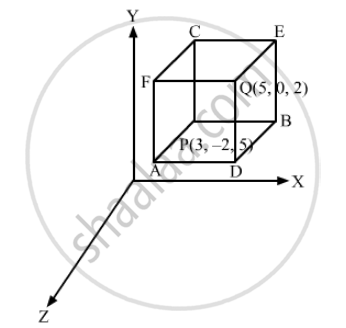
Clearly, PBEC and QDAF are the planes parallel to the yz-plane such that their distances from the yz-plane are 5 and 3, respectively.
\[\therefore\]PA = Distance between planes PBEC and QDAF
= 5\[-\]3
= 2
PB is the distance between planes PAFC and BDQE that are parallel to the zx-plane and are at distances 0 and\[-\]2,respectively, from the zx-plane.
\[\therefore\]PB = 0
\[-\](\[-\]2)
= 2
PC is the distance between parallel planes PBDA and CEQF that are at distances 2 and 5, respectively, from the xy-plane.
\[\therefore\]PC = 2\[-\]5
=\[-\]3
APPEARS IN
RELATED QUESTIONS
Name the octants in which the following points lie:
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (–4, 2, –5), (–4, 2, 5),
(–3, –1, 6), (2, –4, –7).
Coordinate planes divide the space into ______ octants.
Name the octants in which the following points lie:
(–5, –4, 7)
Name the octants in which the following points lie:
(2, –5, –7)
Determine the points in zx-plane are equidistant from the points A(1, –1, 0), B(2, 1, 2) and C(3, 2, –1).
Prove that the triangle formed by joining the three points whose coordinates are (1, 2, 3), (2, 3, 1) and (3, 1, 2) is an equilateral triangle.
Show that the points A(3, 3, 3), B(0, 6, 3), C(1, 7, 7) and D(4, 4, 7) are the vertices of a square.
Find the coordinates of the point which is equidistant from the four points O(0, 0, 0), A(2, 0, 0), B(0, 3, 0) and C(0, 0, 8).
Show that the points (a, b, c), (b, c, a) and (c, a, b) are the vertices of an equilateral triangle.
Verify the following:
(–1, 2, 1), (1, –2, 5), (4, –7, 8) and (2, –3, 4) are vertices of a parallelogram.
Find the locus of the point, the sum of whose distances from the points A(4, 0, 0) and B(–4, 0, 0) is equal to 10.
Write the distance of the point P (2, 3,5) from the xy-plane.
Write the coordinates of the foot of the perpendicular from the point (1, 2, 3) on y-axis.
Write the length of the perpendicular drawn from the point P(3, 5, 12) on x-axis.
Find the point on y-axis which is at a distance of \[\sqrt{10}\] units from the point (1, 2, 3).
Let (3, 4, –1) and (–1, 2, 3) be the end points of a diameter of a sphere. Then, the radius of the sphere is equal to
XOZ-plane divides the join of (2, 3, 1) and (6, 7, 1) in the ratio
What is the locus of a point for which y = 0, z = 0?
The coordinates of the foot of the perpendicular from a point P(6,7, 8) on x - axis are
The perpendicular distance of the point P (6, 7, 8) from xy - plane is
If a line makes an angle of 30°, 60°, 90° with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
If the line drawn from the point (–2, – 1, – 3) meets a plane at right angle at the point (1, – 3, 3), find the equation of the plane
Find the equation of the plane through the points (2, 1, 0), (3, –2, –2) and (3, 1, 7).
Find the equations of the two lines through the origin which intersect the line `(x - 3)/2 = (y - 3)/1 = z/1` at angles of `pi/3` each.
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
Find the equations of the line passing through the point (3,0,1) and parallel to the planes x + 2y = 0 and 3y – z = 0.
The plane ax + by = 0 is rotated about its line of intersection with the plane z = 0 through an angle α. Prove that the equation of the plane in its new position is ax + by `+- (sqrt(a^2 + b^2) tan alpha)z ` = 0
If l1, m1, n1 ; l2, m2, n2 ; l3, m3, n3 are the direction cosines of three mutually perpendicular lines, prove that the line whose direction cosines are proportional to l1 + l2 + l3, m1 + m2 + m3, n1 + n2 + n3 makes equal angles with them.
The plane 2x – 3y + 6z – 11 = 0 makes an angle sin–1(α) with x-axis. The value of α is equal to ______.
The vector equation of the line through the points (3, 4, –7) and (1, –1, 6) is ______.
The cartesian equation of the plane `vecr * (hati + hatj - hatk)` is ______.
The unit vector normal to the plane x + 2y +3z – 6 = 0 is `1/sqrt(14)hati + 2/sqrt(14)hatj + 3/sqrt(14)hatk`.
The intercepts made by the plane 2x – 3y + 5z +4 = 0 on the co-ordinate axis are `-2, 4/3, - 4/5`.
The angle between the line `vecr = (5hati - hatj - 4hatk) + lambda(2hati - hatj + hatk)` and the plane `vec.(3hati - 4hatj - hatk)` + 5 = 0 is `sin^-1(5/(2sqrt(91)))`.
