Advertisements
Advertisements
प्रश्न
In the right-angled triangle QPR, PM is an altitude.
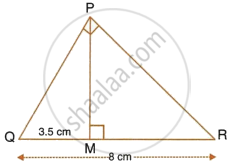
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
उत्तर
In ΔPQM and ΔQPR,
∠PMQ = ∠QPR ...(Each = 90°)
∠Q = ∠Q ...(Common)
∴ ΔPQM ∼ ΔQPR ...(AA postulate)
∴ `(PQ)/(QR) = (QM)/(PQ) = (PM)/(PR)` ...(i)
`\implies` PQ2 = QR × QM
= 8 × 3.5
= 28
∴ `PQ = sqrt(28)` ...(ii)
In ΔPQR, ∠P = 90° and PM ⊥ QR
∴ PM2 = QM × MR = 3.5 × 4.5 ...(∴ MR = QR – QM)
∴ `PM = sqrt(3.5 xx 4.5)` ...(iii)
From (i) `(PQ)/(QR) = (PM)/(PR)`
`sqrt(28)/8 = sqrt(3.5 xx 4.5)/(PR)`
Squaring on both sides,
`28/64 = (3.5 xx 4.5)/(PR)`
`PR^2 = (3.5 xx 4.5 xx 64)/28`
= `(35 xx 45 xx 64)/(10 xx 10 xx 28)`
= `10080/2800`
`=>` PR2 = 36 = (6)2
∴ PR = 6 cm.
APPEARS IN
संबंधित प्रश्न
Given: RS and PT are altitudes of ΔPQR. Prove that:
- ΔPQT ~ ΔQRS,
- PQ × QS = RQ × QT.
In ∆ABC, ∠B = 90° and BD ⊥ AC.
- If CD = 10 cm and BD = 8 cm; find AD.
- If AC = 18 cm and AD = 6 cm; find BD.
- If AC = 9 cm and AB = 7 cm; find AD.
Given : AB || DE and BC || EF. Prove that :
- `(AD)/(DG) = (CF)/(FG)`
- ∆DFG ∼ ∆ACG
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ∆ABC and ∆DEC.
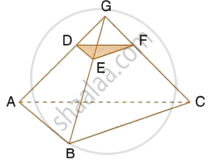
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is
perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
i)`"area of ADC"/"area of FEB"` ii)`"area of ΔAFEB"/"area of ΔABC"`

An aeroplane is 30 m long and its model is 15 cm long. If the total outer surface area of the model is 150 cm2, find the cost of painting the outer surface of the aeroplane at the rate of Rs.120 per sq. m. Given that 50 sq. m of the surface of the aeroplane is left for windows.
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their :
- corresponding medians.
- perimeters.
- areas.
In ΔABC, ∠ACB = 90° and CD ⊥ AB.
Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`
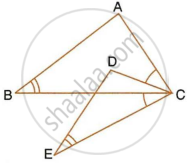
In the give figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that ΔABC ∼ ΔEBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the:
- length of AB
- area of ΔABC

In fig. ABCD is a trapezium in which AB | | DC and AB = 2DC. Determine the ratio between the areas of ΔAOB and ΔCOD.