Advertisements
Advertisements
प्रश्न
कनिका को उसका जेब खर्च 1 जनवरी 2008 को दिया गया। वह इसमें से अपने पिग्गी बैंक में पहले दिन 1 रु डालती है, दूसरे दिन 2 रु डालती है, तीसरे दिन 3 रु डालती है तथा ऐसा ही महीने के अंत तक करती रहती है। उसने अपने जेब खर्च में से 204 रु खर्च भी किए और पाया कि महीने के अंत में उसके पास अभी भी 100 रु शेष हैं। उस महीने उसको कितना जेब खर्च मिला था ?
उत्तर
माना उसकी जेब खर्च ₹ x है।
अब, वह पहले दिन 11 रुपये, दूसरे दिन ₹ 2 रुपये, तीसरे दिन ₹ 3 रुपये और इसी तरह महीने के अंत तक, इन पैसों से अपने गुल्लक में डालती है।
अर्थात, 1 + 2 + 3 + 4 + ... + 31
जो एक AP बनाते हैं जिसमें पद 31 और पहला पद पद = 1 है,
सामान्य अंतर (d) = 2 – 1 = 1
∴ पहले 31 पदों का योग S31 है।
n पदों का योग,
Sn = `n/2[2a + (n - 1)d]`
∴ S31 = `31/2[2 xx 1 + (31 - 1) xx 1]`
= `31/2(2 + 30)`
= `(31 xx 32)/2`
= 31 × 16
= 496
तो, कनिका इस पैसे से महीने के अंत तक ₹ 496 लेती है।
साथ ही, उसने अपनी पॉकेट मनी में से ₹ 204 खर्च किए और पाया कि महीने के अंत में उसके पास अभी भी ₹ 100 हैं।
अब शर्त के अनुसार,
(x – 496) – 204 = 100
⇒ x – 700 = 100
∴ x = ₹ 800
अत:, ₹ 800 महीने के लिए उसकी जेबखर्ची थी।
APPEARS IN
संबंधित प्रश्न
एक A.P. में, a12 = 37 और d = 3 दिया है। a और S12 ज्ञात कीजिए।
एक स्कूल के विद्यार्थियों ने वायु प्रदूषण कम करने के लिए स्कूल के अंदर और बाहर पेड़ लगाने के बारे में सोचा। यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा। उदाहरणार्थ, कक्षा I का एक अनुभाग 1 पेड़ लगाएगा, कक्षा II का एक अनुभाग 2 पेड़ लगाएगा, कक्षा III का एक अनुभाग 3 पेड़ लगाएगा, इत्यादि और ऐसा कक्षा XII तक के लिए चलता रहेगा। प्रत्येक कक्षा के तीन अनुभाग हैं। इस स्कूल के विद्यार्थियों द्वारा लगाए गए कुल पेड़ों की संख्या कितनी होगी?
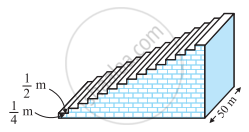
एक फुटबॉल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लंबाई 50 m है और वह ठोस कंक्रीट (concrete) की बनी है। प्रत्येक सीढ़ी में `1/4` m की चढ़ाई है और `1/2` m का फैलाव (चौड़ाई) है। (देखिए आकृति)।इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
[संकेत: पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन = `1/4 xx 1/2 xx 50` m3 है।]
किसी AP में, यदि a = 1, an = 20 और Sn = 399 हों, तो n बराबर ______ है।
योग ज्ञात कीजिए :
1 + (–2) + (–5) + (–8) + ... + (–236)
यदि an = 3 – 4n हो, तो दर्शाइए कि a1, a2, a3,... एक AP बनाते हैं। S20 भी ज्ञात कीजिए।
उस AP के सभी 11 पदों का योग ज्ञात कीजिए, जिसका मध्य पद 30 है।
ज्ञात कीजिए :
1 से 500 तक के उन पूर्णांकों का योग जो 2 या 5 के गुणज हैं।
[संकेत (iii) : ये संख्याएँ होंगी : 2 के गुणज + 5 के गुणज – 2 और 5 दोनों के गुणज]
किसी AP के 11 वें पद का 18 वे पद से अनुपात 2 : 3 है। 5 वें पद का 21 वें पद से अनुपात ज्ञात कीजिए तथा साथ ही प्रथम पाँच पदों के योग का प्रथम 21 पदों के योग से अनुपात ज्ञात कीजिए।
समीकरण – 4 + (−1) + 2 + ... + x = 437 को हल कीजिए।
