Advertisements
Advertisements
प्रश्न
Let A = {−1, 0, 1} and f = {(x, x2) : x ∈ A}. Show that f : A → A is neither one-one nor onto.
उत्तर
A = {−1, 0, 1} and f = {(x, x2) : x ∈ A}
Given, f(x) = x2
Injectivity :
f(1) = 12=1 and
f(-1)=(-1)2=1
⇒ 1 and -1 have the same images.
So, f is not one-one.
Surjectivity :
Co-domain of f = {-1, 0, 1}
f(1) = 12 = 1,
f(-1) = (-1)2 = 1 and
f(0) = 0
⇒ Range of f = {0, 1}
So, both are not same.
Hence, f is not onto
APPEARS IN
संबंधित प्रश्न
Show that the function f: ℝ → ℝ defined by f(x) = `x/(x^2 + 1), ∀x in R`is neither one-one nor onto. Also, if g: ℝ → ℝ is defined as g(x) = 2x - 1. Find fog(x)
If the function `f(x) = sqrt(2x - 3)` is invertible then find its inverse. Hence prove that `(fof^(-1))(x) = x`
Which of the following functions from A to B are one-one and onto?
f1 = {(1, 3), (2, 5), (3, 7)} ; A = {1, 2, 3}, B = {3, 5, 7}
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = |x|
If f : A → B is an injection, such that range of f = {a}, determine the number of elements in A.
Let A = [-1, 1]. Then, discuss whether the following function from A to itself is one-one, onto or bijective : g(x) = |x|
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
If f : A → B and g : B → C are one-one functions, show that gof is a one-one function.
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
If f, g : R → R be two functions defined as f(x) = |x| + x and g(x) = |x|- x, ∀x∈R" .Then find fog and gof. Hence find fog(–3), fog(5) and gof (–2).
If f : R → (0, 2) defined by `f (x) =(e^x - e^(x))/(e^x +e^(-x))+1`is invertible , find f-1.
Let \[f : \left( - \frac{\pi}{2}, \frac{\pi}{2} \right) \to R\] be a function defined by f(x) = cos [x]. Write range (f).
Let f : R → R be defined as `f (x) = (2x - 3)/4.` write fo f-1 (1) .
If f : {5, 6} → {2, 3} and g : {2, 3} → {5, 6} are given by f = {(5, 2), (6, 3)} and g = {(2, 5), (3, 6)}, then find fog. [NCERT EXEMPLAR]
\[f : R \to R \text{given by} f\left( x \right) = x + \sqrt{x^2} \text{ is }\]
Let the function
\[f : R - \left\{ - b \right\} \to R - \left\{ 1 \right\}\]
\[f\left( x \right) = \frac{x + a}{x + b}, a \neq b .\text{Then},\]
Which of the following functions from
to itself are bijections?
Let
\[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function,
\[f : A \to A\] given by
\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] Then, for what value of α is \[f \left( f\left( x \right) \right) = x?\]
If \[f : R \to R\] is given by \[f\left( x \right) = x^3 + 3, \text{then} f^{- 1} \left( x \right)\] is equal to
Write about strlen() function.
Let the function f: R → R be defined by f(x) = 4x – 1, ∀ x ∈ R. Then, show that f is one-one.
Let f, g: R → R be two functions defined as f(x) = |x| + x and g(x) = x – x ∀ x ∈ R. Then, find f o g and g o f
The domain of the function f: R → R defined by f(x) = `sqrt(x^2 - 3x + 2)` is ______
Are the following set of ordered pairs functions? If so, examine whether the mapping is injective or surjective.
{(x, y): x is a person, y is the mother of x}
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
k = {(1,4), (2, 5)}
Let A = R – {3}, B = R – {1}. Let f: A → B be defined by f(x) = `(x - 2)/(x - 3)` ∀ x ∈ A . Then show that f is bijective
Let f: R → R be defined by f(x) = `1/x` ∀ x ∈ R. Then f is ______.
The function f : R → R defined by f(x) = 3 – 4x is ____________.
The number of bijective functions from set A to itself when A contains 106 elements is ____________.
Which of the following functions from Z into Z is bijective?
Let X = {-1, 0, 1}, Y = {0, 2} and a function f : X → Y defiend by y = 2x4, is ____________.
Let g(x) = x2 – 4x – 5, then ____________.
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever

Let I be the set of all citizens of India who were eligible to exercise their voting right in the general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(V1, V2) ∶ V1, V2 ∈ I and both use their voting right in the general election - 2019}
- Mr. ’X’ and his wife ‘W’ both exercised their voting right in the general election-2019, Which of the following is true?
Sherlin and Danju are playing Ludo at home during Covid-19. While rolling the dice, Sherlin’s sister Raji observed and noted the possible outcomes of the throw every time belongs to set {1,2,3,4,5,6}. Let A be the set of players while B be the set of all possible outcomes.
A = {S, D}, B = {1,2,3,4,5,6}
- Raji wants to know the number of functions from A to B. How many number of functions are possible?
The solution set of the inequation log1/3(x2 + x + 1) + 1 > 0 is ______.
Let a function `f: N rightarrow N` be defined by
f(n) = `{:[(2n",", n = 2"," 4"," 6"," 8","......),(n - 1",", n = 3"," 7"," 11"," 15","......),((n + 1)/2",", n = 1"," 5"," 9"," 13","......):}`
then f is ______.
Which one of the following graphs is a function of x?
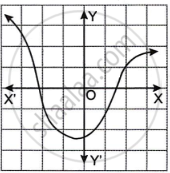 |
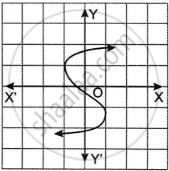 |
| Graph A | Graph B |
