Advertisements
Advertisements
प्रश्न
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
px + qy = p - q
qx - py = p + q
उत्तर
चूंकि px + qy = p - q ⇒ px + qy - (p - q) = 0 ….(1)
एवं qx - py = p + q ⇒ qx - py - (p + q) = 0 ….(2)
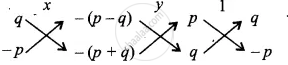
⇒ `x/(-p[-(p - q)] - q[-(p + q)]) = y/(-(p + q).p - [-p(p - q).q]) = 1/(q^2 + p^2)`
⇒ `x/(p^2 - pq + pq + q^2) = y/(-p^2 - pq + pq - q^2) = 1/(p^2 + q^2)`
⇒ `x/(p^2 + q^2) = (-y)/(p^2 + q^2) = 1/(p^2 + q^2)`
⇒ x = `(p^2 + q^2)/(p^2 + q^2) = 1` एवं y = `-(p^2 + q^2)/(p^2 + q^2) = -1`
अतः दत्त समीकरण युग्म का अभीष्ट हल x = 1 एवं y = -1 है।
APPEARS IN
संबंधित प्रश्न
अनुपातों `a_1/a_2, b_1/b_2` और `c_1/c_2` की तुलना कर ज्ञात कीजिए कि निम्न समीकरण युग्म द्वारा निरूपण रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं, समांतर हैं अथवा संपाती हैं:
6x - 3y + 10 = 0
2x - y + 9 = 0
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
ax + by = c
bx + ay = 1 + c
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए:
152x - 378y = -74
-378x + 152y = -604
c का वह मान, जिसके लिए समीकरणों cx – y = 2 और 6x – 2y = 3 के युग्म के अपरिमित रूप से अनेक हल होंगे, है ______।
एक अद्वितीय हल x = 2, y = –3 वाले समीकरण का एक युग्म है ______।
निम्नलिखित समीकरण-युग्मों (i) से (iv) में p और (v) में p तथा q के मान ज्ञात कीजिए :
– x + py = 1 और px – y = 1,
यदि समीकरण-युग्म का कोई हल नहीं है।
निम्नलिखित समीकरण-युग्मों (i) से (iv) में p और (v) में p तथा q के मान ज्ञात कीजिए :
– 3x + 5y = 7 और 2px – 3y = 1
यदि इन समीकरणों द्वारा निरूपित रेखाएँ एक अद्वितीय बिंदु पर प्रतिच्छेद करती हैं।
निम्नलिखित समीकरण-युग्मों (i) से (iv) में p और (v) में p तथा q के मान ज्ञात कीजिए :
2x + 3y = 7 और 2px + py = 28 – qy,
यदि समीकरण-युग्म के अपरिमित रूप से अनेक हल हैं।
यदि 2x + y = 23 और 4x – y = 19 है, तो 5y – 2x और `y/x - 2` के मान ज्ञात कीजिए।
4 पेन और 4 पेंसिल बॉक्सों का मूल्य 100 रु है। एक पेन के मूल्य का तीन गुना एक पेंसिल बॉक्स के मूल्य से 15 रु अधिक है। उपरोक्त स्थिति के लिए, रैखिक समीकरणों का एक युग्म बनाइए। एक पेन और एक पेंसिल बॉक्स के मूल्य भी ज्ञात कीजिए।
