Advertisements
Advertisements
प्रश्न
A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y+ 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.
उत्तर
AB and BC are two linear paths. Equations of lines AB and BC
2x – 3y + 4 = 0 ....(i)
And 3x + 4y – 5 = 0 ......(ii)
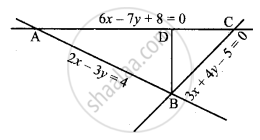
AB and BC meet at point B.
On multiplying equation (i) by 3 and equation (ii) by 2
6x – 9y = –12 ....(iii)
6x + 8y = 10 .....(iv)
By subtracting equation (iii) from equation (iv),
17y = 10 + 12 = 22
∴ y = `22/7`
Putting the value of y in equation (i),
`2"x" - 3 xx (22/17) = -4`
or `2"x" = -4 + 66/17 = (-2)/17`
∴ x = `-1/17`
Thus the coordinates of B are `((-1)/17, 22/17)`.
To reach from B to AC in minimum time the minimum distance to be covered is BD (BD ⊥ AC).
Equation of line AC, slope of 6x – 7y + 8 = 0 = `6/7`
Slope of BD = `-7/6`
BD passes through point B `((-1)/17, 22/17)`.
∴ Equation of line BD
y – y1 = m(x – x1)
`"y" - 22/17 = -7/6 ("x" + 1/17)`
On multiplying by 102,
102y – 132 = –119x – 7
119x + 102y – 125 = 0
Therefore, to reach AC from B, we have to take path BD whose equation is 119x + 102y – 125 = 0.
APPEARS IN
संबंधित प्रश्न
Reduce the following equation into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
`x – sqrt3y + 8 = 0`
In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
If three lines whose equations are y = m1x + c1, y = m2x + c2 and y = m3x + c3 are concurrent, then show that m1(c2 – c3) + m2 (c3 – c1) + m3 (c1 – c2) = 0.
Show that the equation of the line passing through the origin and making an angle θ with the line `y = mx + c " is " y/c = (m+- tan theta)/(1 +- m tan theta)`.
In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?
Find the equation of a line which is equidistant from the lines x = − 2 and x = 6.
Find the equation of a line which makes an angle of tan−1 (3) with the x-axis and cuts off an intercept of 4 units on negative direction of y-axis.
Find the equation of the straight line on which the length of the perpendicular from the origin is 2 and the perpendicular makes an angle α with x-axis such that sin α = \[\frac{1}{3}\].
Find the equation of the straight line upon which the length of the perpendicular from the origin is 2 and the slope of this perpendicular is \[\frac{5}{12}\].
If the straight line through the point P (3, 4) makes an angle π/6 with the x-axis and meets the line 12x + 5y + 10 = 0 at Q, find the length PQ.
Reduce the following equation to the normal form and find p and α in \[x + \sqrt{3}y - 4 = 0\] .
Reduce the following equation to the normal form and find p and α in \[x - y + 2\sqrt{2} = 0\].
Find the coordinates of the vertices of a triangle, the equations of whose sides are x + y − 4 = 0, 2x − y + 3 = 0 and x − 3y + 2 = 0.
Find the coordinates of the vertices of a triangle, the equations of whose sides are
y (t1 + t2) = 2x + 2a t1t2, y (t2 + t3) = 2x + 2a t2t3 and, y (t3 + t1) = 2x + 2a t1t3.
Find the area of the triangle formed by the line y = 0, x = 2 and x + 2y = 3.
Find the area of the triangle formed by the line x + y − 6 = 0, x − 3y − 2 = 0 and 5x − 3y + 2 = 0.
Find the equation of the line joining the point (3, 5) to the point of intersection of the lines 4x + y − 1 = 0 and 7x − 3y − 35 = 0.
Find the conditions that the straight lines y = m1 x + c1, y = m2 x + c2 and y = m3 x + c3 may meet in a point.
If the lines p1 x + q1 y = 1, p2 x + q2 y = 1 and p3 x + q3 y = 1 be concurrent, show that the points (p1, q1), (p2, q2) and (p3, q3) are collinear.
Show that the straight lines L1 = (b + c) x + ay + 1 = 0, L2 = (c + a) x + by + 1 = 0 and L3 = (a + b) x + cy + 1 = 0 are concurrent.
Find the equation of the straight line perpendicular to 2x − 3y = 5 and cutting off an intercept 1 on the positive direction of the x-axis.
Find the equation of the right bisector of the line segment joining the points (a, b) and (a1, b1).
Find the projection of the point (1, 0) on the line joining the points (−1, 2) and (5, 4).
Write the coordinates of the orthocentre of the triangle formed by the lines xy = 0 and x + y = 1.
If a ≠ b ≠ c, write the condition for which the equations (b − c) x + (c − a) y + (a − b) = 0 and (b3 − c3) x + (c3 − a3) y + (a3 − b3) = 0 represent the same line.
The number of real values of λ for which the lines x − 2y + 3 = 0, λx + 3y + 1 = 0 and 4x − λy + 2 = 0 are concurrent is
A point equidistant from the line 4x + 3y + 10 = 0, 5x − 12y + 26 = 0 and 7x+ 24y − 50 = 0 is
The inclination of the line x – y + 3 = 0 with the positive direction of x-axis is ______.
Find the equation of the straight line which passes through the point (1, – 2) and cuts off equal intercepts from axes.
If the intercept of a line between the coordinate axes is divided by the point (–5, 4) in the ratio 1 : 2, then find the equation of the line.
A line cutting off intercept – 3 from the y-axis and the tangent at angle to the x-axis is `3/5`, its equation is ______.
If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2), then the equation of the line will be ______.
For specifying a straight line, how many geometrical parameters should be known?
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is ______.
Reduce the following equation into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
x − y = 4
