Advertisements
Advertisements
प्रश्न
Can a triangle have All angles less than 60° Justify your answer in case.
उत्तर
No,
Having all angles less than `60^@` will make that sum less than `180^@`which is not
possible.
[ The sum of all the internal angles of a triangle is`180^@`]
APPEARS IN
संबंधित प्रश्न
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

In ΔABC, ∠B = ∠C and ray AX bisects the exterior angle ∠DAC. If ∠DAX = 70°, then ∠ACB =
State, if the triangle is possible with the following angles :
20°, 70°, and 90°
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
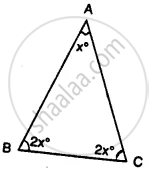
Find the value of the angle in the given figure:
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.
In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
